 Attention Mechanisms
Attention Mechanisms
Adaptive Masking
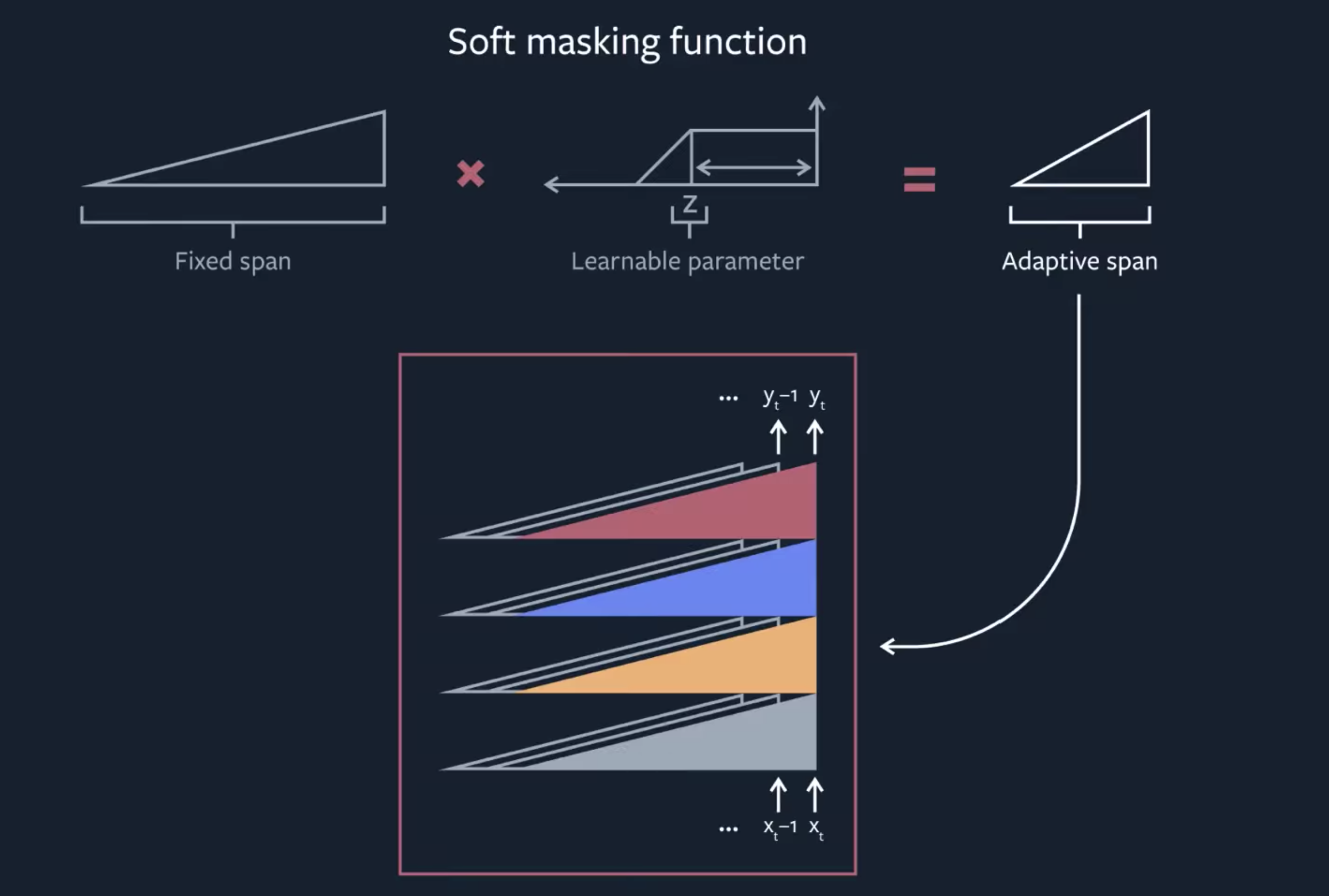
Introduced by Sukhbaatar et al. in Adaptive Attention Span in TransformersAdaptive Masking is a type of attention mechanism that allows a model to learn its own context size to attend over. For each head in Multi-Head Attention, a masking function is added to control for the span of the attention. A masking function is a non-increasing function that maps a distance to a value in $\left[0, 1\right]$. Adaptive masking takes the following soft masking function $m_{z}$ parametrized by a real value $z$ in $\left[0, S\right]$:
$$ m_{z}\left(x\right) = \min\left[\max\left[\frac{1}{R}\left(R+z-x\right), 0\right], 1\right] $$
where $R$ is a hyper-parameter that controls its softness. The shape of this piecewise function as a function of the distance. This soft masking function is inspired by Jernite et al. (2017). The attention weights from are then computed on the masked span:
$$ a_{tr} = \frac{m_{z}\left(t-r\right)\exp\left(s_{tr}\right)}{\sum^{t-1}_{q=t-S}m_{z}\left(t-q\right)\exp\left(s_{tq}\right)}$$
A $\mathcal{l}_{1}$ penalization is added on the parameters $z_{i}$ for each attention head $i$ of the model to the loss function:
$$ L = - \log{P}\left(w_{1}, \dots, w_{T}\right) + \frac{\lambda}{M}\sum_{i}z_{i} $$
where $\lambda > 0$ is the regularization hyperparameter, and $M$ is the number of heads in each layer. This formulation is differentiable in the parameters $z_{i}$, and learnt jointly with the rest of the model.
Source: Adaptive Attention Span in TransformersPapers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Language Modelling | 5 | 13.16% |
| Translation | 3 | 7.89% |
| Image Segmentation | 2 | 5.26% |
| Medical Image Segmentation | 2 | 5.26% |
| Semantic Segmentation | 2 | 5.26% |
| Machine Translation | 2 | 5.26% |
| Self-Supervised Learning | 2 | 5.26% |
| Computational Efficiency | 1 | 2.63% |
| Decision Making | 1 | 2.63% |
 L1 Regularization
L1 Regularization