Loss Functions
Loss Functions
Balanced L1 Loss
Introduced by Pang et al. in Libra R-CNN: Towards Balanced Learning for Object DetectionBalanced L1 Loss is a loss function used for the object detection task. Classification and localization problems are solved simultaneously under the guidance of a multi-task loss since Fast R-CNN, defined as:
$$ L_{p,u,t_{u},v} = L_{cls}\left(p, u\right) + \lambda\left[u \geq 1\right]L_{loc}\left(t^{u}, v\right) $$
$L_{cls}$ and $L_{loc}$ are objective functions corresponding to recognition and localization respectively. Predictions and targets in $L_{cls}$ are denoted as $p$ and $u$. $t_{u}$ is the corresponding regression results with class $u$. $v$ is the regression target. $\lambda$ is used for tuning the loss weight under multi-task learning. We call samples with a loss greater than or equal to 1.0 outliers. The other samples are called inliers.
A natural solution for balancing the involved tasks is to tune the loss weights of them. However, owing to the unbounded regression targets, directly raising the weight of localization loss will make the model more sensitive to outliers. These outliers, which can be regarded as hard samples, will produce excessively large gradients that are harmful to the training process. The inliers, which can be regarded as the easy samples, contribute little gradient to the overall gradients compared with the outliers. To be more specific, inliers only contribute 30% gradients average per sample compared with outliers. Considering these issues, the authors introduced the balanced L1 loss, which is denoted as $L_{b}$.
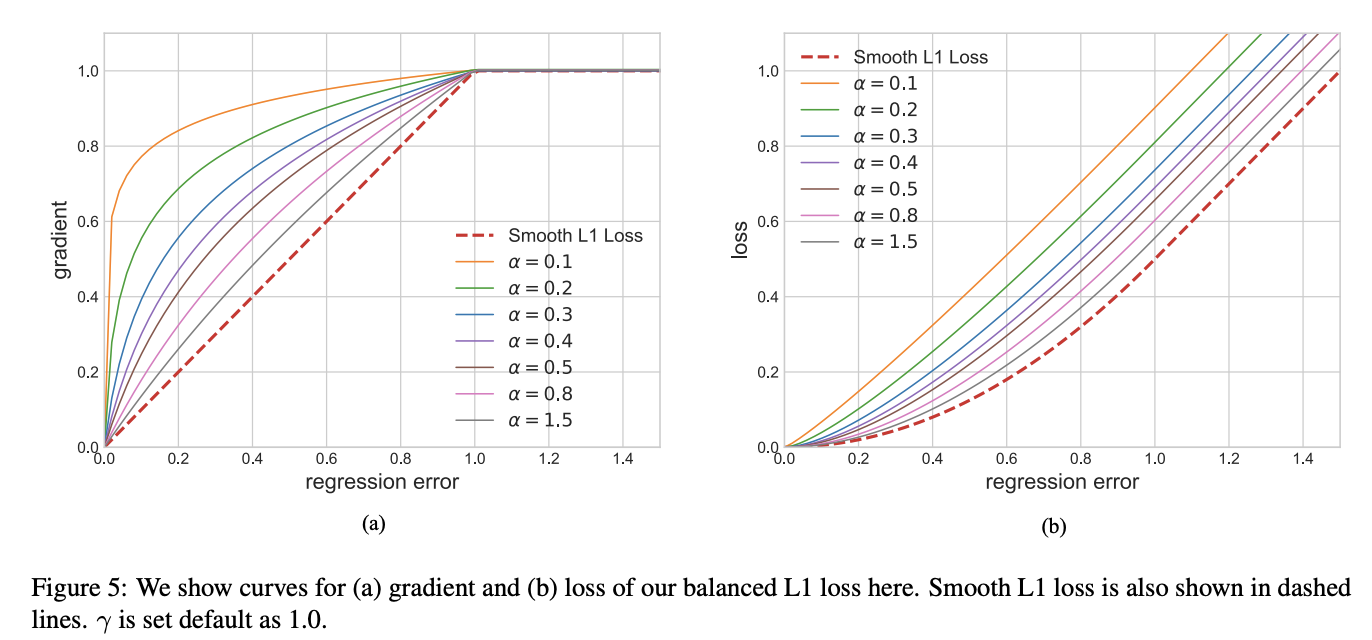
Balanced L1 loss is derived from the conventional smooth L1 loss, in which an inflection point is set to separate inliers from outliners, and clip the large gradients produced by outliers with a maximum value of 1.0, as shown by the dashed lines in the Figure to the right. The key idea of balanced L1 loss is promoting the crucial regression gradients, i.e. gradients from inliers (accurate samples), to rebalance the involved samples and tasks, thus achieving a more balanced training within classification, overall localization and accurate localization. Localization loss $L_{loc}$ uses balanced L1 loss is defined as:
$$ L_{loc} = \sum_{i\in{x,y,w,h}}L_{b}\left(t^{u}_{i}-v_{i}\right) $$
The Figure to the right shows that the balanced L1 loss increases the gradients of inliers under the control of a factor denoted as $\alpha$. A small $\alpha$ increases more gradient for inliers, but the gradients of outliers are not influenced. Besides, an overall promotion magnification controlled by γ is also brought in for tuning the upper bound of regression errors, which can help the objective function better balancing involved tasks. The two factors that control different aspects are mutually enhanced to reach a more balanced training.$b$ is used to ensure $L_{b}\left(x = 1\right)$ has the same value for both formulations in the equation below.
By integrating the gradient formulation above, we can get the balanced L1 loss as:
$$ L_{b}\left(x\right) = \frac{\alpha}{b}\left(b|x| + 1\right)ln\left(b|x| + 1\right) - \alpha|x| \text{ if } |x| < 1$$
$$ L_{b}\left(x\right) = \gamma|x| + C \text{ otherwise } $$
in which the parameters $\gamma$, $\alpha$, and $b$ are constrained by $\alpha\text{ln}\left(b + 1\right) = \gamma$. The default parameters are set as $\alpha = 0.5$ and $\gamma = 1.5$
Source: Libra R-CNN: Towards Balanced Learning for Object DetectionPapers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Object Detection | 2 | 28.57% |
| Nutrition | 1 | 14.29% |
| Ensemble Learning | 1 | 14.29% |
| Medical Object Detection | 1 | 14.29% |
| Food recommendation | 1 | 14.29% |
| Object Localization | 1 | 14.29% |
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
| 🤖 No Components Found | You can add them if they exist; e.g. Mask R-CNN uses RoIAlign |