Time Series Analysis
Time Series Analysis
Dynamic Time Warping
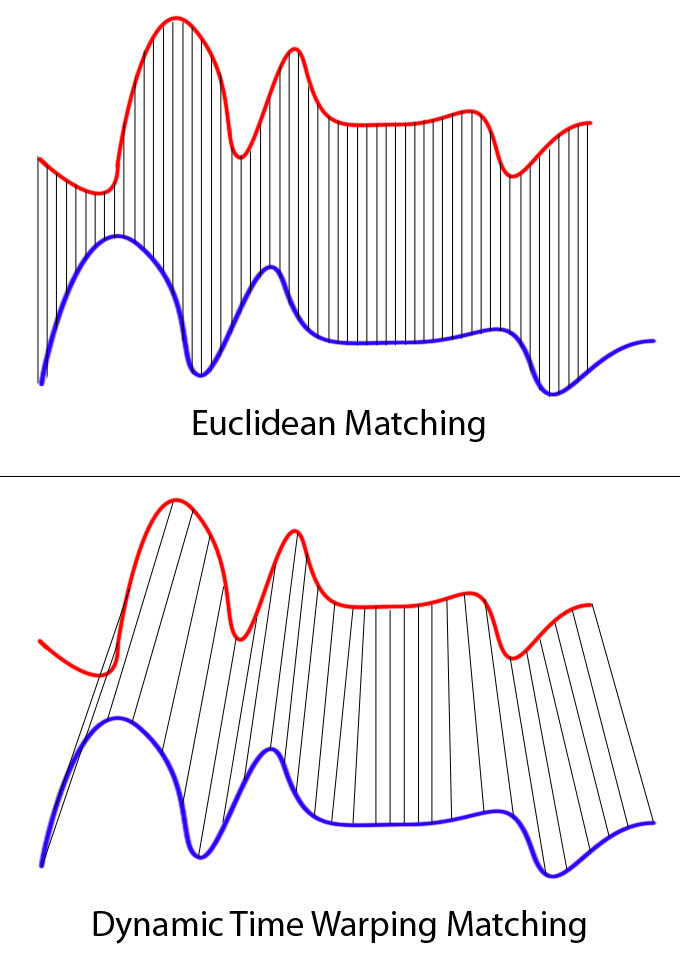
Dynamic Time Warping (DTW) [1] is one of well-known distance measures between a pairwise of time series. The main idea of DTW is to compute the distance from the matching of similar elements between time series. It uses the dynamic programming technique to find the optimal temporal matching between elements of two time series.
For instance, similarities in walking could be detected using DTW, even if one person was walking faster than the other, or if there were accelerations and decelerations during the course of an observation. DTW has been applied to temporal sequences of video, audio, and graphics data — indeed, any data that can be turned into a linear sequence can be analyzed with DTW. A well known application has been automatic speech recognition, to cope with different speaking speeds. Other applications include speaker recognition and online signature recognition. It can also be used in partial shape matching application.
In general, DTW is a method that calculates an optimal match between two given sequences (e.g. time series) with certain restriction and rules:
- Every index from the first sequence must be matched with one or more indices from the other sequence, and vice versa
- The first index from the first sequence must be matched with the first index from the other sequence (but it does not have to be its only match)
- The last index from the first sequence must be matched with the last index from the other sequence (but it does not have to be its only match)
- The mapping of the indices from the first sequence to indices from the other sequence must be monotonically increasing, and vice versa, i.e. if j>i are indices from the first sequence, then there must not be two indices l>k in the other sequence, such that index i is matched with index l and index j is matched with index k, and vice versa.
[1] Sakoe, Hiroaki, and Seibi Chiba. "Dynamic programming algorithm optimization for spoken word recognition." IEEE transactions on acoustics, speech, and signal processing 26, no. 1 (1978): 43-49.
Papers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Dynamic Time Warping | 114 | 27.74% |
| Time Series Analysis | 71 | 17.27% |
| Clustering | 26 | 6.33% |
| Time Series Classification | 20 | 4.87% |
| General Classification | 17 | 4.14% |
| Classification | 11 | 2.68% |
| Anomaly Detection | 9 | 2.19% |
| Action Recognition | 6 | 1.46% |
| Time Series Clustering | 6 | 1.46% |
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
| 🤖 No Components Found | You can add them if they exist; e.g. Mask R-CNN uses RoIAlign |