Stochastic Optimization
Stochastic Optimization
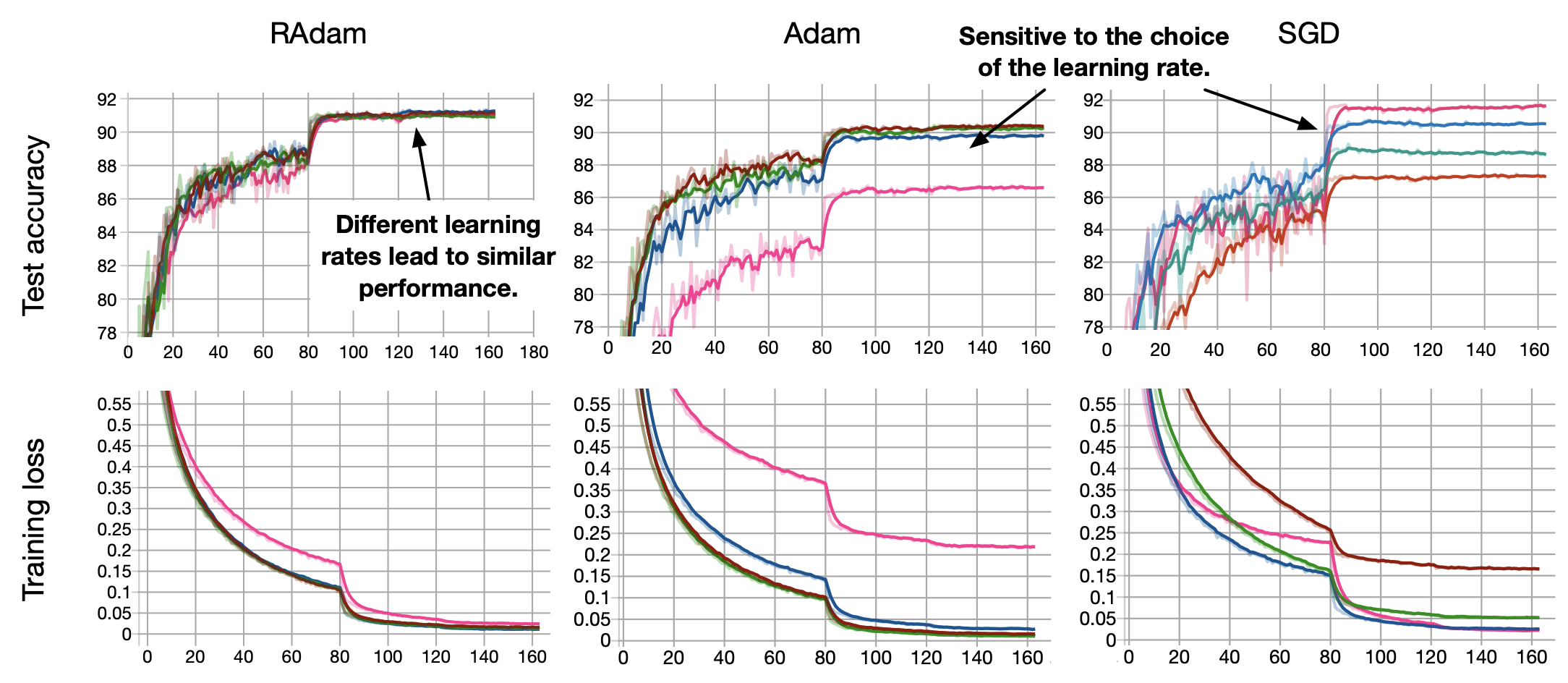
RAdam
Introduced by Liu et al. in On the Variance of the Adaptive Learning Rate and BeyondRectified Adam, or RAdam, is a variant of the Adam stochastic optimizer that introduces a term to rectify the variance of the adaptive learning rate. It seeks to tackle the bad convergence problem suffered by Adam. The authors argue that the root cause of this behaviour is that the adaptive learning rate has undesirably large variance in the early stage of model training, due to the limited amount of training samples being used. Thus, to reduce such variance, it is better to use smaller learning rates in the first few epochs of training - which justifies the warmup heuristic. This heuristic motivates RAdam which rectifies the variance problem:
$$g_{t} = \nabla_{\theta}f_{t}\left(\theta_{t-1}\right) $$
$$v_{t} = 1/\beta_{2}v_{t-1} + \left(1-\beta_{2}\right)g^{2}_{t} $$
$$m_{t} = \beta_{1}m_{t-1} + \left(1-\beta_{1}\right)g_{t} $$
$$ \hat{m_{t}} = m_{t} / \left(1-\beta^{t}_{1}\right) $$
$$ \rho_{t} = \rho_{\infty} - 2t\beta^{t}_{2}/\left(1-\beta^{t}_{2}\right) $$
$$\rho_{\infty} = \frac{2}{1-\beta_2} - 1$$
If the variance is tractable - $\rho_{t} > 4$ then:
...the adaptive learning rate is computed as:
$$ l_{t} = \sqrt{\left(1-\beta^{t}_{2}\right)/v_{t}}$$
...the variance rectification term is calculated as:
$$ r_{t} = \sqrt{\frac{(\rho_{t}-4)(\rho_{t}-2)\rho_{\infty}}{(\rho_{\infty}-4)(\rho_{\infty}-2)\rho_{t}}}$$
...and we update parameters with adaptive momentum:
$$ \theta_{t} = \theta_{t-1} - \alpha_{t}r_{t}\hat{m}_{t}l_{t} $$
If the variance isn't tractable we update instead with:
$$ \theta_{t} = \theta_{t-1} - \alpha_{t}\hat{m}_{t} $$
Source: On the Variance of the Adaptive Learning Rate and BeyondPapers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Language Modelling | 4 | 8.70% |
| Image Classification | 3 | 6.52% |
| Autonomous Driving | 2 | 4.35% |
| BIG-bench Machine Learning | 2 | 4.35% |
| Translation | 2 | 4.35% |
| Classification | 2 | 4.35% |
| General Classification | 2 | 4.35% |
| Machine Translation | 2 | 4.35% |
| Autonomous Vehicles | 1 | 2.17% |
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
| 🤖 No Components Found | You can add them if they exist; e.g. Mask R-CNN uses RoIAlign |