Attention Modules
Attention Modules
SAGAN Self-Attention Module
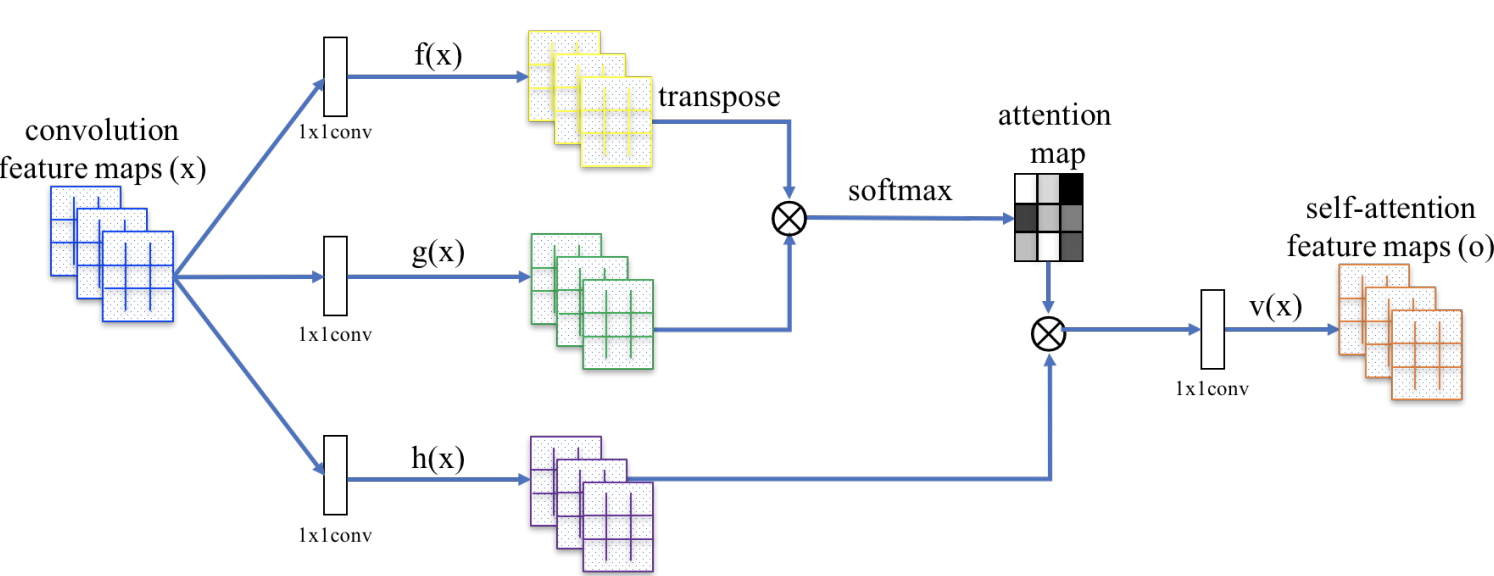
Introduced by Zhang et al. in Self-Attention Generative Adversarial NetworksThe SAGAN Self-Attention Module is a self-attention module used in the Self-Attention GAN architecture for image synthesis. In the module, image features from the previous hidden layer $\textbf{x} \in \mathbb{R}^{C\text{x}N}$ are first transformed into two feature spaces $\textbf{f}$, $\textbf{g}$ to calculate the attention, where $\textbf{f(x) = W}_{\textbf{f}}{\textbf{x}}$, $\textbf{g}(\textbf{x})=\textbf{W}_{\textbf{g}}\textbf{x}$. We then calculate:
$$\beta_{j, i} = \frac{\exp\left(s_{ij}\right)}{\sum^{N}_{i=1}\exp\left(s_{ij}\right)} $$
$$ \text{where } s_{ij} = \textbf{f}(\textbf{x}_{i})^{T}\textbf{g}(\textbf{x}_{i}) $$
and $\beta_{j, i}$ indicates the extent to which the model attends to the $i$th location when synthesizing the $j$th region. Here, $C$ is the number of channels and $N$ is the number of feature locations of features from the previous hidden layer. The output of the attention layer is $\textbf{o} = \left(\textbf{o}_{\textbf{1}}, \textbf{o}_{\textbf{2}}, \ldots, \textbf{o}_{\textbf{j}} , \ldots, \textbf{o}_{\textbf{N}}\right) \in \mathbb{R}^{C\text{x}N}$ , where,
$$ \textbf{o}_{\textbf{j}} = \textbf{v}\left(\sum^{N}_{i=1}\beta_{j, i}\textbf{h}\left(\textbf{x}_{\textbf{i}}\right)\right) $$
$$ \textbf{h}\left(\textbf{x}_{\textbf{i}}\right) = \textbf{W}_{\textbf{h}}\textbf{x}_{\textbf{i}} $$
$$ \textbf{v}\left(\textbf{x}_{\textbf{i}}\right) = \textbf{W}_{\textbf{v}}\textbf{x}_{\textbf{i}} $$
In the above formulation, $\textbf{W}_{\textbf{g}} \in \mathbb{R}^{\bar{C}\text{x}C}$, $\mathbf{W}_{f} \in \mathbb{R}^{\bar{C}\text{x}C}$, $\textbf{W}_{\textbf{h}} \in \mathbb{R}^{\bar{C}\text{x}C}$ and $\textbf{W}_{\textbf{v}} \in \mathbb{R}^{C\text{x}\bar{C}}$ are the learned weight matrices, which are implemented as $1$×$1$ convolutions. The authors choose $\bar{C} = C/8$.
In addition, the module further multiplies the output of the attention layer by a scale parameter and adds back the input feature map. Therefore, the final output is given by,
$$\textbf{y}_{\textbf{i}} = \gamma\textbf{o}_{\textbf{i}} + \textbf{x}_{\textbf{i}}$$
where $\gamma$ is a learnable scalar and it is initialized as 0. Introducing $\gamma$ allows the network to first rely on the cues in the local neighborhood – since this is easier – and then gradually learn to assign more weight to the non-local evidence.
Source: Self-Attention Generative Adversarial NetworksPapers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Image Generation | 40 | 18.96% |
| Conditional Image Generation | 17 | 8.06% |
| Multi-agent Reinforcement Learning | 7 | 3.32% |
| Super-Resolution | 6 | 2.84% |
| Reinforcement Learning (RL) | 6 | 2.84% |
| Image-to-Image Translation | 6 | 2.84% |
| Translation | 6 | 2.84% |
| Decision Making | 5 | 2.37% |
| Denoising | 4 | 1.90% |
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
 1x1 Convolution
1x1 Convolution
|
Convolutions | |
 Dot-Product Attention
Dot-Product Attention
|
Attention Mechanisms | |
 Softmax
Softmax
|
Output Functions |