Loss Functions
Loss Functions
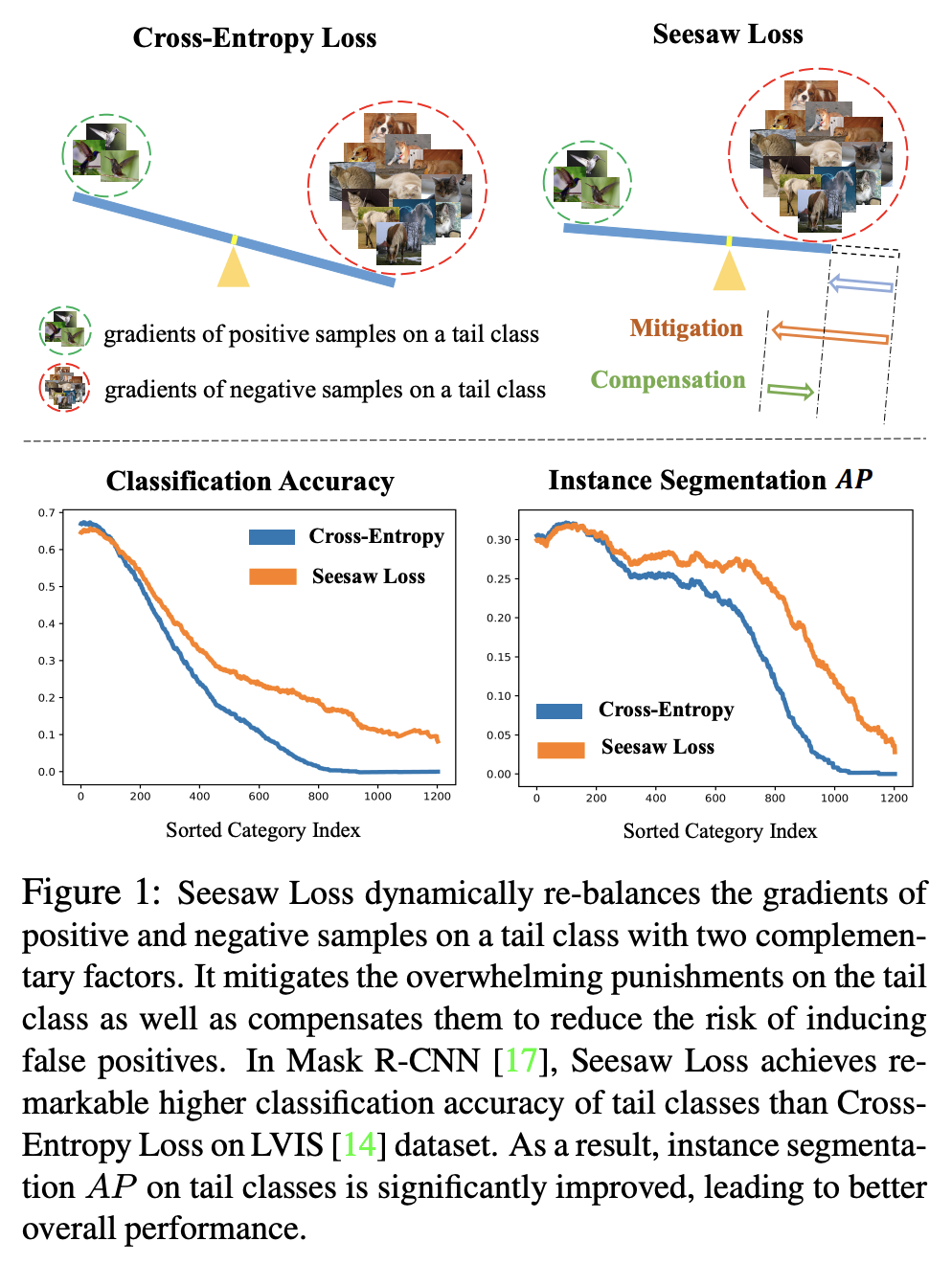
Seesaw Loss
Introduced by Wang et al. in Seesaw Loss for Long-Tailed Instance SegmentationSeesaw Loss is a loss function for long-tailed instance segmentation. It dynamically re-balances the gradients of positive and negative samples on a tail class with two complementary factors: mitigation factor and compensation factor. The mitigation factor reduces punishments to tail categories w.r.t the ratio of cumulative training instances between different categories. Meanwhile, the compensation factor increases the penalty of misclassified instances to avoid false positives of tail categories. The synergy of the two factors enables Seesaw Loss to mitigate the overwhelming punishments on tail classes as well as compensate for the risk of misclassification caused by diminished penalties.
$$ L_{seesaw}\left(\mathbf{x}\right) = - \sum^{C}_{i=1}y_{i}\log\left(\hat{\sigma}_{i}\right) $$
$$ \text{with } \hat{\sigma_{i}} = \frac{e^{z_{i}}}{- \sum^{C}_{j\neq{1}}\mathcal{S}_{ij}e^{z_{j}}+e^{z_{i}} } $$
Here $\mathcal{S}_{ij}$ works as a tunable balancing factor between different classes. By a careful design of $\mathcal{S}_{ij}$, Seesaw loss adjusts the punishments on class j from positive samples of class $i$. Seesaw loss determines $\mathcal{S}_{ij}$ by a mitigation factor and a compensation factor, as:
$$ \mathcal{S}_{ij} =\mathcal{M}_{ij} · \mathcal{C}_{ij} $$
The mitigation factor $\mathcal{M}_{ij}$ decreases the penalty on tail class $j$ according to a ratio of instance numbers between tail class $j$ and head class $i$. The compensation factor $\mathcal{C}_{ij}$ increases the penalty on class $j$ whenever an instance of class $i$ is misclassified to class $j$.
Source: Seesaw Loss for Long-Tailed Instance SegmentationPapers
| Paper | Code | Results | Date | Stars |
|---|
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
| 🤖 No Components Found | You can add them if they exist; e.g. Mask R-CNN uses RoIAlign |