A physics-aware, probabilistic machine learning framework for coarse-graining high-dimensional systems in the Small Data regime
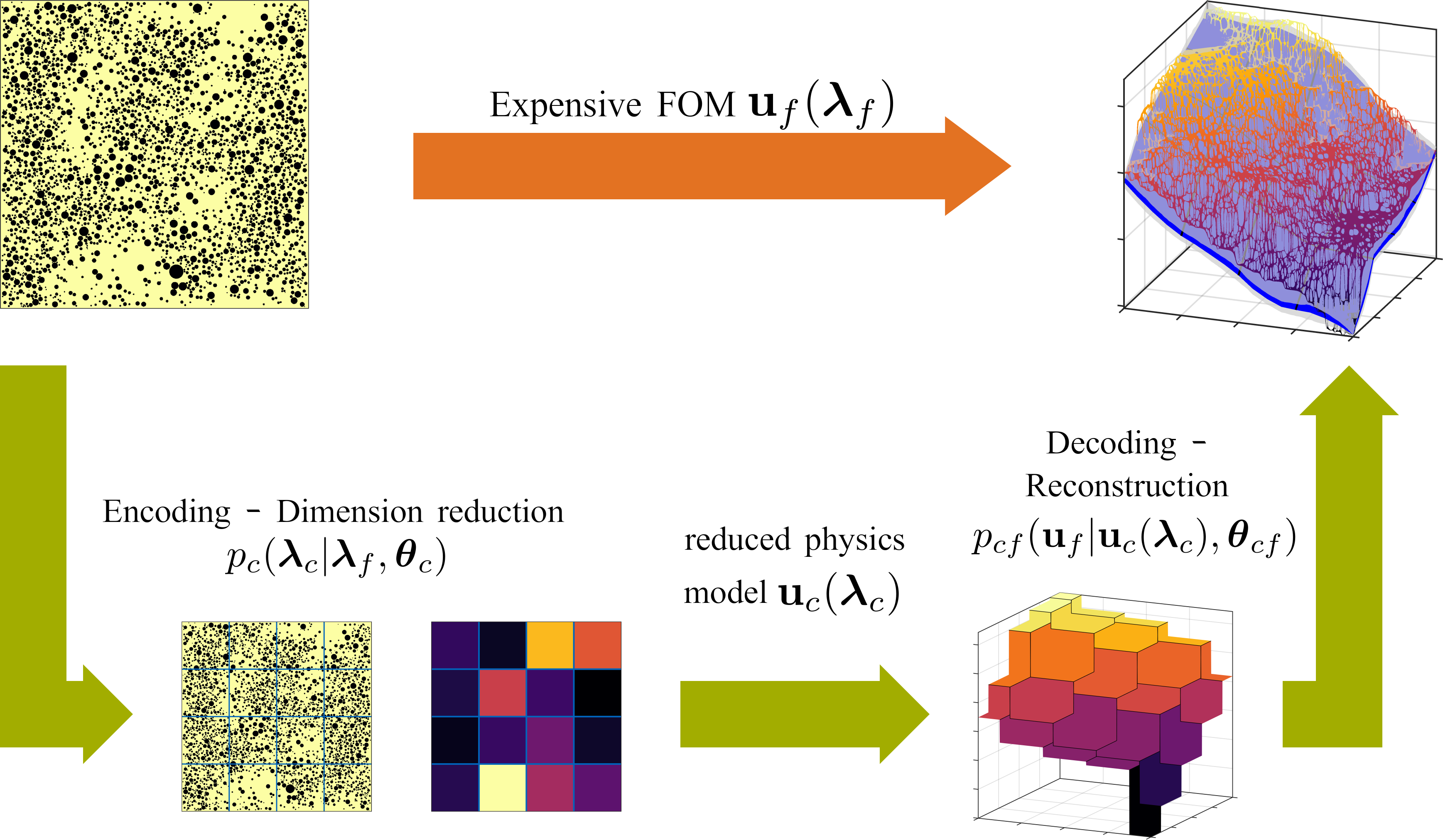
The automated construction of coarse-grained models represents a pivotal component in computer simulation of physical systems and is a key enabler in various analysis and design tasks related to uncertainty quantification. Pertinent methods are severely inhibited by the high-dimension of the parametric input and the limited number of training input/output pairs that can be generated when computationally demanding forward models are considered. Such cases are frequently encountered in the modeling of random heterogeneous media where the scale of the microstructure necessitates the use of high-dimensional random vectors and very fine discretizations of the governing equations. The present paper proposes a probabilistic Machine Learning framework that is capable of operating in the presence of Small Data by exploiting aspects of the physical structure of the problem as well as contextual knowledge. As a result, it can perform comparably well under extrapolative conditions. It unifies the tasks of dimensionality and model-order reduction through an encoder-decoder scheme that simultaneously identifies a sparse set of salient lower-dimensional microstructural features and calibrates an inexpensive, coarse-grained model which is predictive of the output. Information loss is accounted for and quantified in the form of probabilistic predictive estimates. The learning engine is based on Stochastic Variational Inference. We demonstrate how the variational objectives can be used not only to train the coarse-grained model, but also to suggest refinements that lead to improved predictions.
PDF Abstract