Adaptive Propagation Graph Convolutional Network
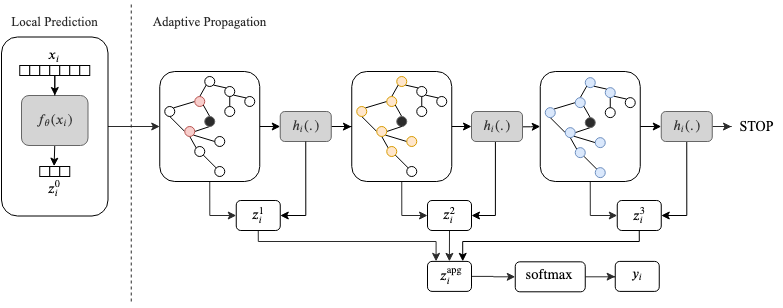
Graph convolutional networks (GCNs) are a family of neural network models that perform inference on graph data by interleaving vertex-wise operations and message-passing exchanges across nodes. Concerning the latter, two key questions arise: (i) how to design a differentiable exchange protocol (e.g., a 1-hop Laplacian smoothing in the original GCN), and (ii) how to characterize the trade-off in complexity with respect to the local updates. In this paper, we show that state-of-the-art results can be achieved by adapting the number of communication steps independently at every node. In particular, we endow each node with a halting unit (inspired by Graves' adaptive computation time) that after every exchange decides whether to continue communicating or not. We show that the proposed adaptive propagation GCN (AP-GCN) achieves superior or similar results to the best proposed models so far on a number of benchmarks, while requiring a small overhead in terms of additional parameters. We also investigate a regularization term to enforce an explicit trade-off between communication and accuracy. The code for the AP-GCN experiments is released as an open-source library.
PDF Abstract