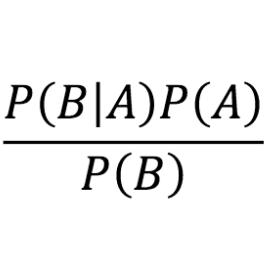Adversarial Message Passing For Graphical Models
Bayesian inference on structured models typically relies on the ability to infer posterior distributions of underlying hidden variables. However, inference in implicit models or complex posterior distributions is hard. A popular tool for learning implicit models are generative adversarial networks (GANs) which learn parameters of generators by fooling discriminators. Typically, GANs are considered to be models themselves and are not understood in the context of inference. Current techniques rely on inefficient global discrimination of joint distributions to perform learning, or only consider discriminating a single output variable. We overcome these limitations by treating GANs as a basis for likelihood-free inference in generative models and generalize them to Bayesian posterior inference over factor graphs. We propose local learning rules based on message passing minimizing a global divergence criterion involving cooperating local adversaries used to sidestep explicit likelihood evaluations. This allows us to compose models and yields a unified inference and learning framework for adversarial learning. Our framework treats model specification and inference separately and facilitates richly structured models within the family of Directed Acyclic Graphs, including components such as intractable likelihoods, non-differentiable models, simulators and generally cumbersome models. A key result of our treatment is the insight that Bayesian inference on structured models can be performed only with sampling and discrimination when using nonparametric variational families, without access to explicit distributions. As a side-result, we discuss the link to likelihood maximization. These approaches hold promise to be useful in the toolbox of probabilistic modelers and enrich the gamut of current probabilistic programming applications.
PDF Abstract