ANODE: Unconditionally Accurate Memory-Efficient Gradients for Neural ODEs
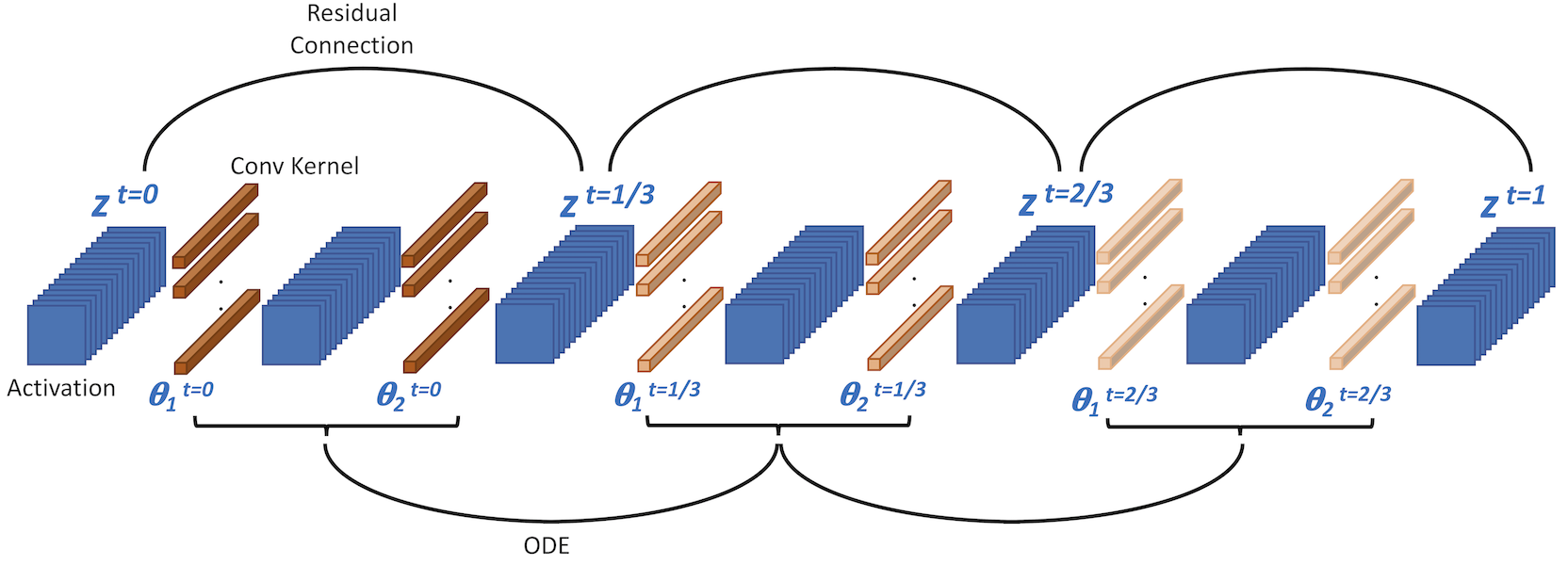
Residual neural networks can be viewed as the forward Euler discretization of an Ordinary Differential Equation (ODE) with a unit time step. This has recently motivated researchers to explore other discretization approaches and train ODE based networks. However, an important challenge of neural ODEs is their prohibitive memory cost during gradient backpropogation. Recently a method proposed in [8], claimed that this memory overhead can be reduced from O(LN_t), where N_t is the number of time steps, down to O(L) by solving forward ODE backwards in time, where L is the depth of the network. However, we will show that this approach may lead to several problems: (i) it may be numerically unstable for ReLU/non-ReLU activations and general convolution operators, and (ii) the proposed optimize-then-discretize approach may lead to divergent training due to inconsistent gradients for small time step sizes. We discuss the underlying problems, and to address them we propose ANODE, an Adjoint based Neural ODE framework which avoids the numerical instability related problems noted above, and provides unconditionally accurate gradients. ANODE has a memory footprint of O(L) + O(N_t), with the same computational cost as reversing ODE solve. We furthermore, discuss a memory efficient algorithm which can further reduce this footprint with a trade-off of additional computational cost. We show results on Cifar-10/100 datasets using ResNet and SqueezeNext neural networks.
PDF Abstract