Bayesian Probabilistic Numerical Integration with Tree-Based Models
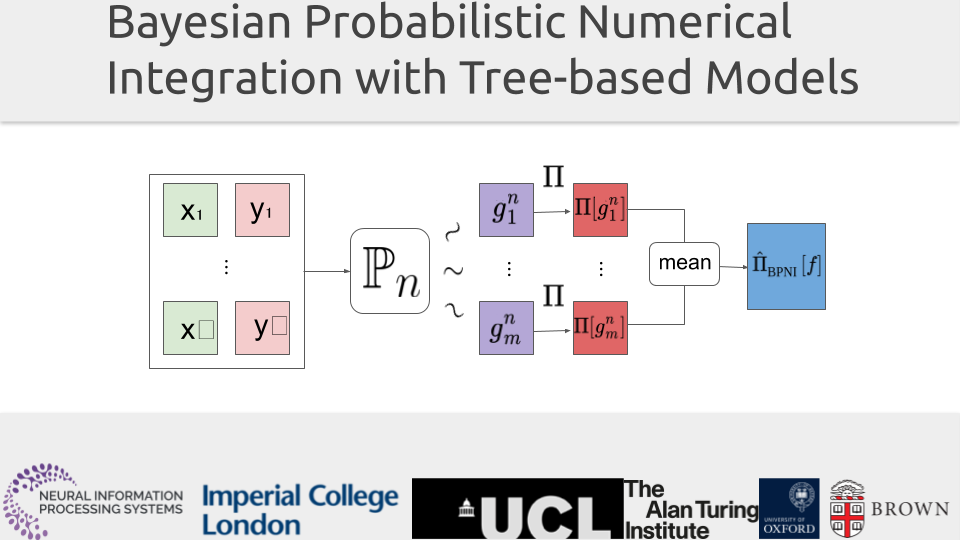
Bayesian quadrature (BQ) is a method for solving numerical integration problems in a Bayesian manner, which allows users to quantify their uncertainty about the solution. The standard approach to BQ is based on a Gaussian process (GP) approximation of the integrand. As a result, BQ is inherently limited to cases where GP approximations can be done in an efficient manner, thus often prohibiting very high-dimensional or non-smooth target functions. This paper proposes to tackle this issue with a new Bayesian numerical integration algorithm based on Bayesian Additive Regression Trees (BART) priors, which we call BART-Int. BART priors are easy to tune and well-suited for discontinuous functions. We demonstrate that they also lend themselves naturally to a sequential design setting and that explicit convergence rates can be obtained in a variety of settings. The advantages and disadvantages of this new methodology are highlighted on a set of benchmark tests including the Genz functions, and on a Bayesian survey design problem.
PDF Abstract NeurIPS 2020 PDF NeurIPS 2020 Abstract