Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers
Recurrent neural networks (RNNs), temporal convolutions, and neural differential equations (NDEs) are popular families of deep learning models for time-series data, each with unique strengths and tradeoffs in modeling power and computational efficiency. We introduce a simple sequence model inspired by control systems that generalizes these approaches while addressing their shortcomings. The Linear State-Space Layer (LSSL) maps a sequence $u \mapsto y$ by simply simulating a linear continuous-time state-space representation $\dot{x} = Ax + Bu, y = Cx + Du$. Theoretically, we show that LSSL models are closely related to the three aforementioned families of models and inherit their strengths. For example, they generalize convolutions to continuous-time, explain common RNN heuristics, and share features of NDEs such as time-scale adaptation. We then incorporate and generalize recent theory on continuous-time memorization to introduce a trainable subset of structured matrices $A$ that endow LSSLs with long-range memory. Empirically, stacking LSSL layers into a simple deep neural network obtains state-of-the-art results across time series benchmarks for long dependencies in sequential image classification, real-world healthcare regression tasks, and speech. On a difficult speech classification task with length-16000 sequences, LSSL outperforms prior approaches by 24 accuracy points, and even outperforms baselines that use hand-crafted features on 100x shorter sequences.
PDF Abstract NeurIPS 2021 PDF NeurIPS 2021 Abstract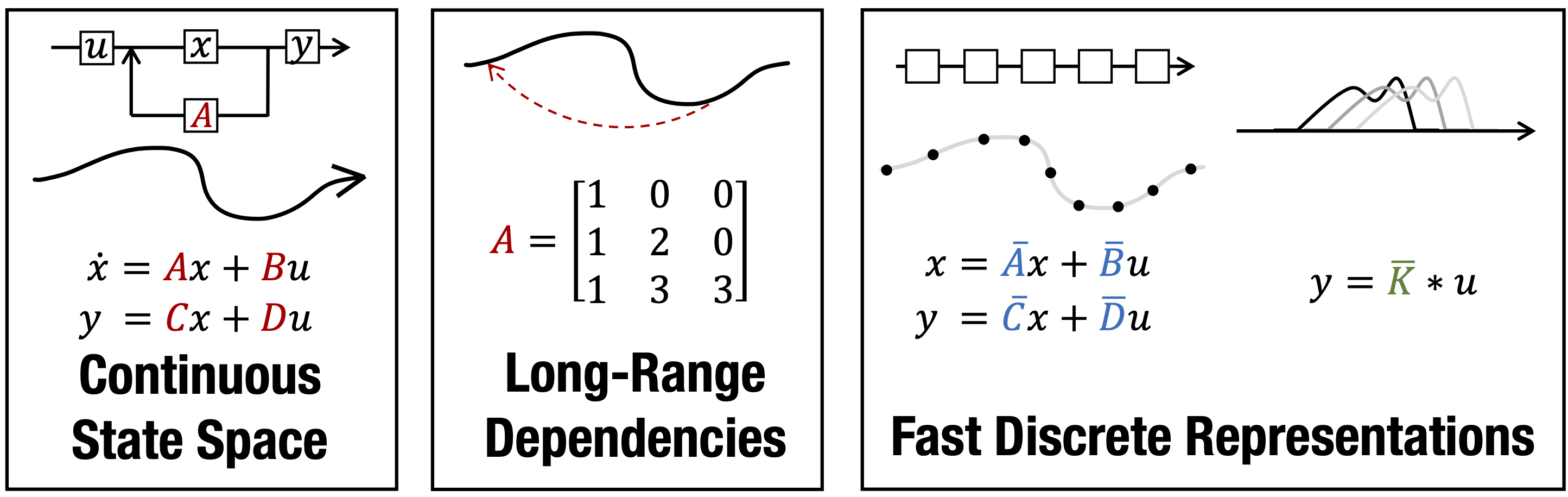







 MNIST
MNIST
 CelebA
CelebA
