Completely Self-Supervised Crowd Counting via Distribution Matching
Dense crowd counting is a challenging task that demands millions of head annotations for training models. Though existing self-supervised approaches could learn good representations, they require some labeled data to map these features to the end task of density estimation. We mitigate this issue with the proposed paradigm of complete self-supervision, which does not need even a single labeled image. The only input required to train, apart from a large set of unlabeled crowd images, is the approximate upper limit of the crowd count for the given dataset. Our method dwells on the idea that natural crowds follow a power law distribution, which could be leveraged to yield error signals for backpropagation. A density regressor is first pretrained with self-supervision and then the distribution of predictions is matched to the prior by optimizing Sinkhorn distance between the two. Experiments show that this results in effective learning of crowd features and delivers significant counting performance. Furthermore, we establish the superiority of our method in less data setting as well. The code and models for our approach is available at https://github.com/val-iisc/css-ccnn.
PDF Abstract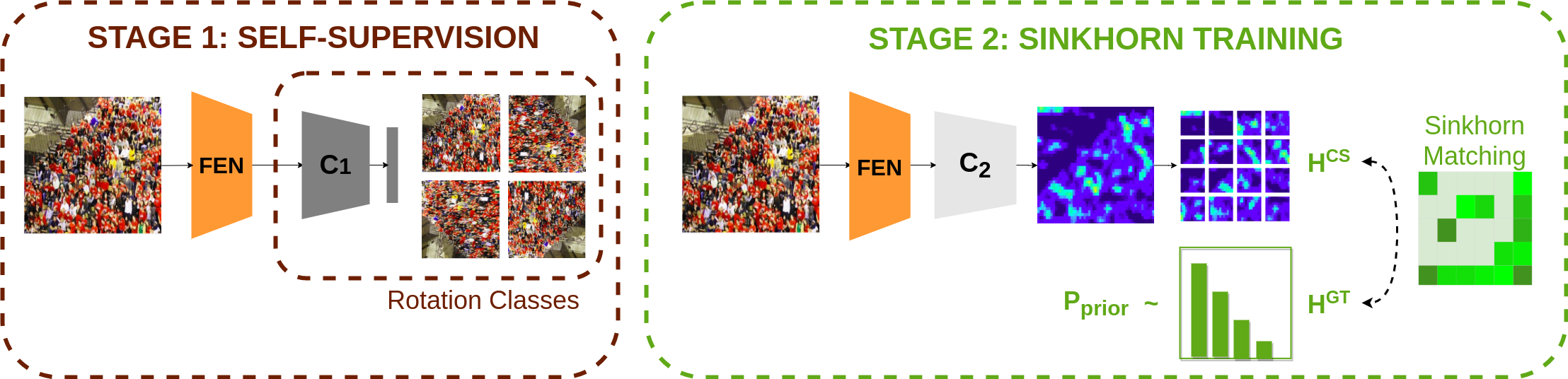


 ShanghaiTech
ShanghaiTech
 UCF-QNRF
UCF-QNRF
 JHU-CROWD
JHU-CROWD