Deep Learning and Symbolic Regression for Discovering Parametric Equations
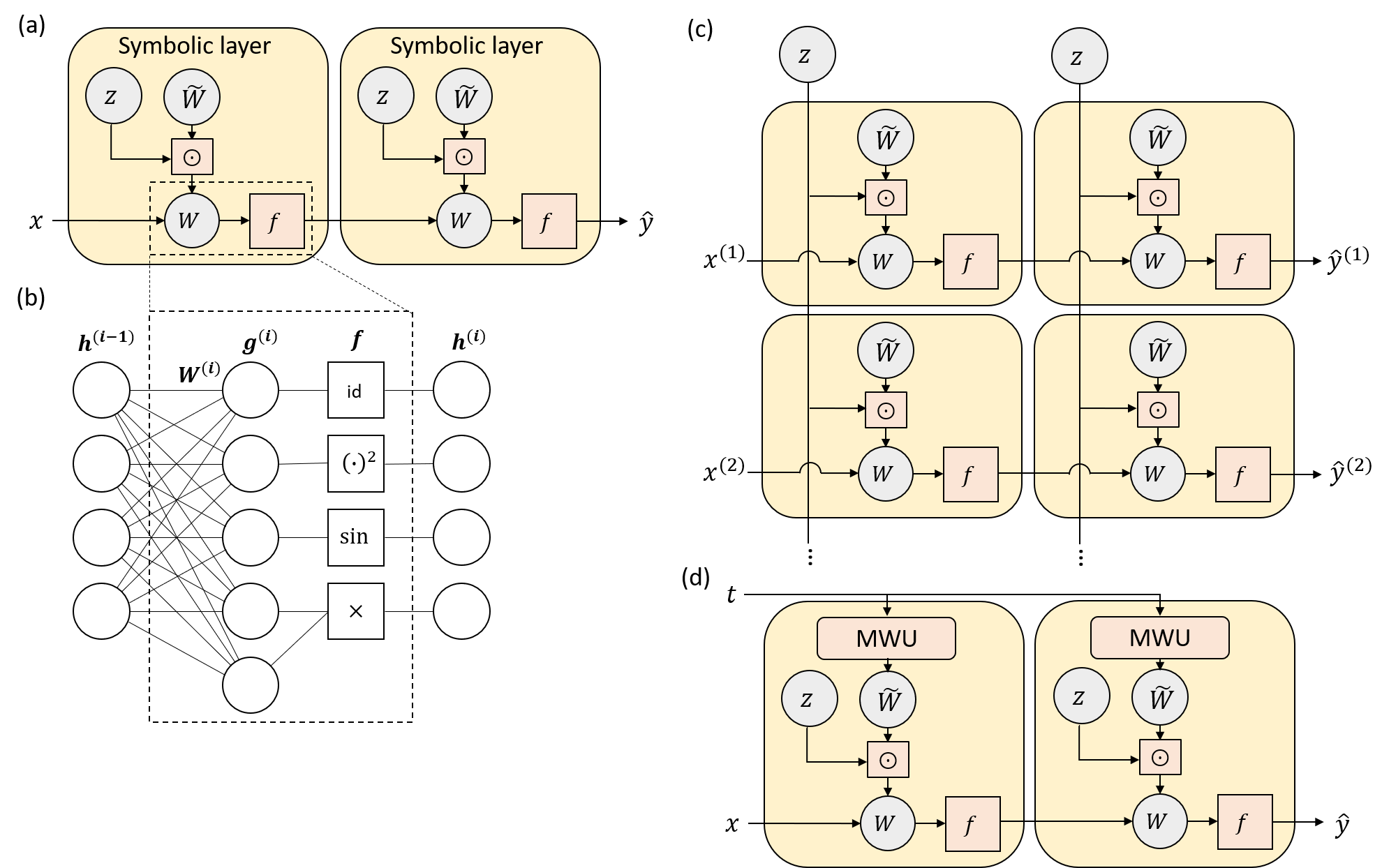
Symbolic regression is a machine learning technique that can learn the governing formulas of data and thus has the potential to transform scientific discovery. However, symbolic regression is still limited in the complexity and dimensionality of the systems that it can analyze. Deep learning on the other hand has transformed machine learning in its ability to analyze extremely complex and high-dimensional datasets. We propose a neural network architecture to extend symbolic regression to parametric systems where some coefficient may vary but the structure of the underlying governing equation remains constant. We demonstrate our method on various analytic expressions, ODEs, and PDEs with varying coefficients and show that it extrapolates well outside of the training domain. The neural network-based architecture can also integrate with other deep learning architectures so that it can analyze high-dimensional data while being trained end-to-end. To this end we integrate our architecture with convolutional neural networks to analyze 1D images of varying spring systems.
PDF Abstract