Equivariant Spherical Deconvolution: Learning Sparse Orientation Distribution Functions from Spherical Data
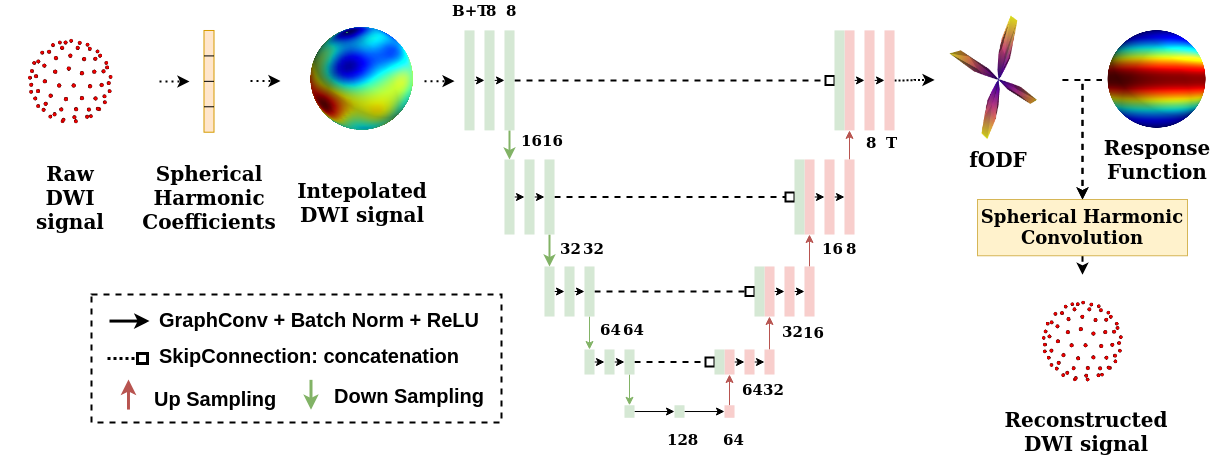
We present a rotation-equivariant unsupervised learning framework for the sparse deconvolution of non-negative scalar fields defined on the unit sphere. Spherical signals with multiple peaks naturally arise in Diffusion MRI (dMRI), where each voxel consists of one or more signal sources corresponding to anisotropic tissue structure such as white matter. Due to spatial and spectral partial voluming, clinically-feasible dMRI struggles to resolve crossing-fiber white matter configurations, leading to extensive development in spherical deconvolution methodology to recover underlying fiber directions. However, these methods are typically linear and struggle with small crossing-angles and partial volume fraction estimation. In this work, we improve on current methodologies by nonlinearly estimating fiber structures via unsupervised spherical convolutional networks with guaranteed equivariance to spherical rotation. Experimentally, we first validate our proposition via extensive single and multi-shell synthetic benchmarks demonstrating competitive performance against common baselines. We then show improved downstream performance on fiber tractography measures on the Tractometer benchmark dataset. Finally, we show downstream improvements in terms of tractography and partial volume estimation on a multi-shell dataset of human subjects.
PDF Abstract