Functional optimal transport: map estimation and domain adaptation for functional data
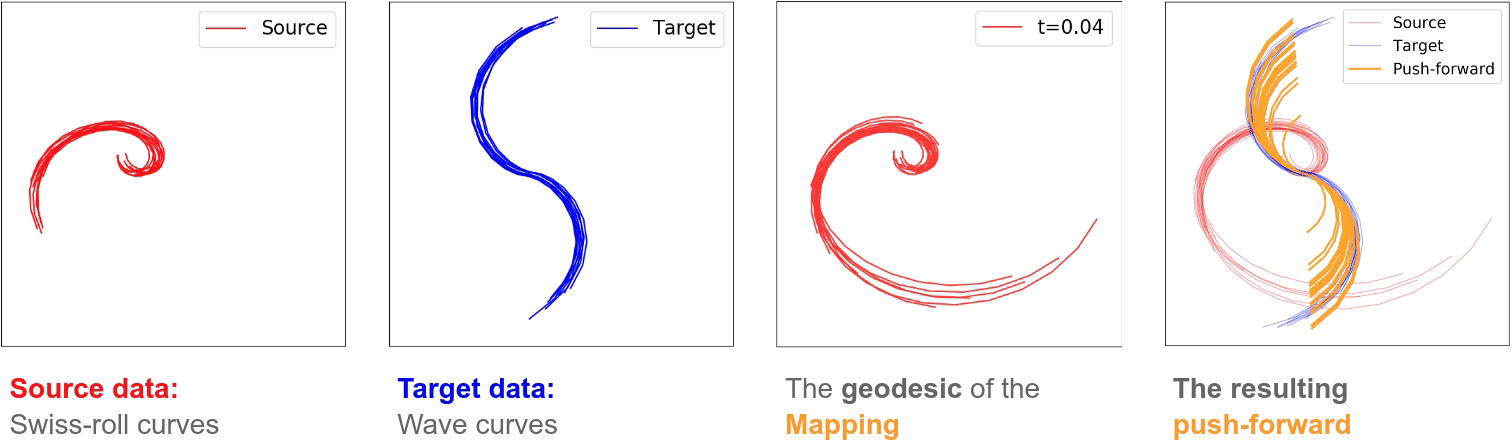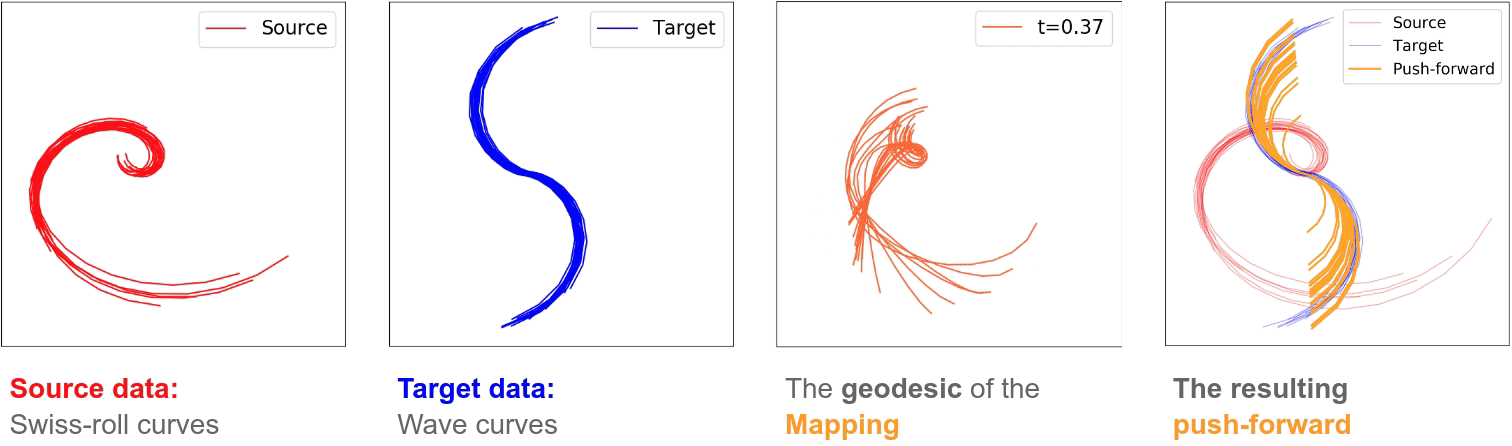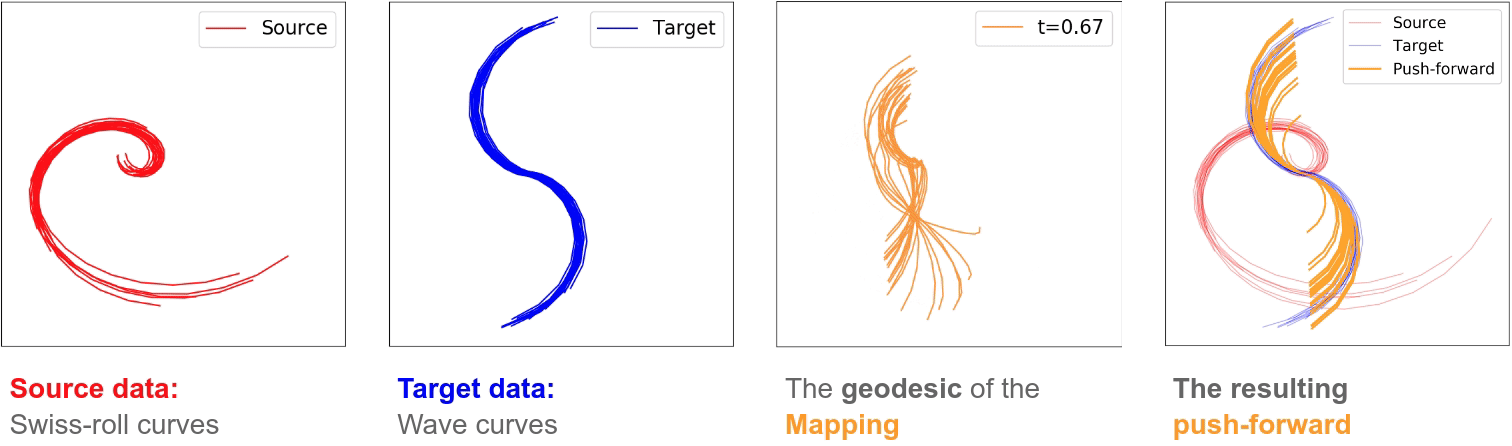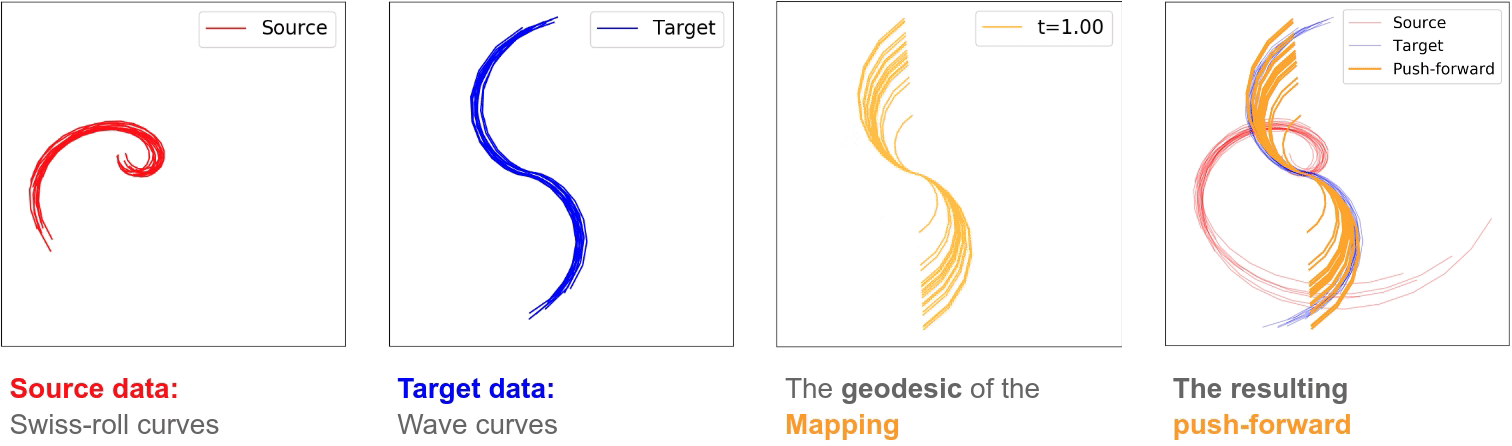
We introduce a formulation of optimal transport problem for distributions on function spaces, where the stochastic map between functional domains can be partially represented in terms of an (infinite-dimensional) Hilbert-Schmidt operator mapping a Hilbert space of functions to another. For numerous machine learning tasks, data can be naturally viewed as samples drawn from spaces of functions, such as curves and surfaces, in high dimensions. Optimal transport for functional data analysis provides a useful framework of treatment for such domains. { Since probability measures in infinite dimensional spaces generally lack absolute continuity (that is, with respect to non-degenerate Gaussian measures), the Monge map in the standard optimal transport theory for finite dimensional spaces may not exist. Our approach to the optimal transport problem in infinite dimensions is by a suitable regularization technique -- we restrict the class of transport maps to be a Hilbert-Schmidt space of operators.} To this end, we develop an efficient algorithm for finding the stochastic transport map between functional domains and provide theoretical guarantees on the existence, uniqueness, and consistency of our estimate for the Hilbert-Schmidt operator. We validate our method on synthetic datasets and examine the functional properties of the transport map. Experiments on real-world datasets of robot arm trajectories further demonstrate the effectiveness of our method on applications in domain adaptation.
PDF Abstract