Graph Embedding with Hierarchical Attentive Membership
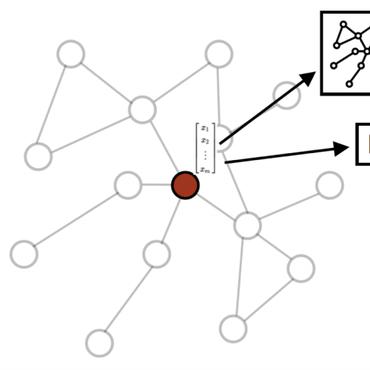
The exploitation of graph structures is the key to effectively learning representations of nodes that preserve useful information in graphs. A remarkable property of graph is that a latent hierarchical grouping of nodes exists in a global perspective, where each node manifests its membership to a specific group based on the context composed by its neighboring nodes. Most prior works ignore such latent groups and nodes' membership to different groups, not to mention the hierarchy, when modeling the neighborhood structure. Thus, they fall short of delivering a comprehensive understanding of the nodes under different contexts in a graph. In this paper, we propose a novel hierarchical attentive membership model for graph embedding, where the latent memberships for each node are dynamically discovered based on its neighboring context. Both group-level and individual-level attentions are performed when aggregating neighboring states to generate node embeddings. We introduce structural constraints to explicitly regularize the inferred memberships of each node, such that a well-defined hierarchical grouping structure is captured. The proposed model outperformed a set of state-of-the-art graph embedding solutions on node classification and link prediction tasks in a variety of graphs including citation networks and social networks. Qualitative evaluations visualize the learned node embeddings along with the inferred memberships, which proved the concept of membership hierarchy and enables explainable embedding learning in graphs.
PDF Abstract