Hierarchical Deep Learning of Multiscale Differential Equation Time-Steppers
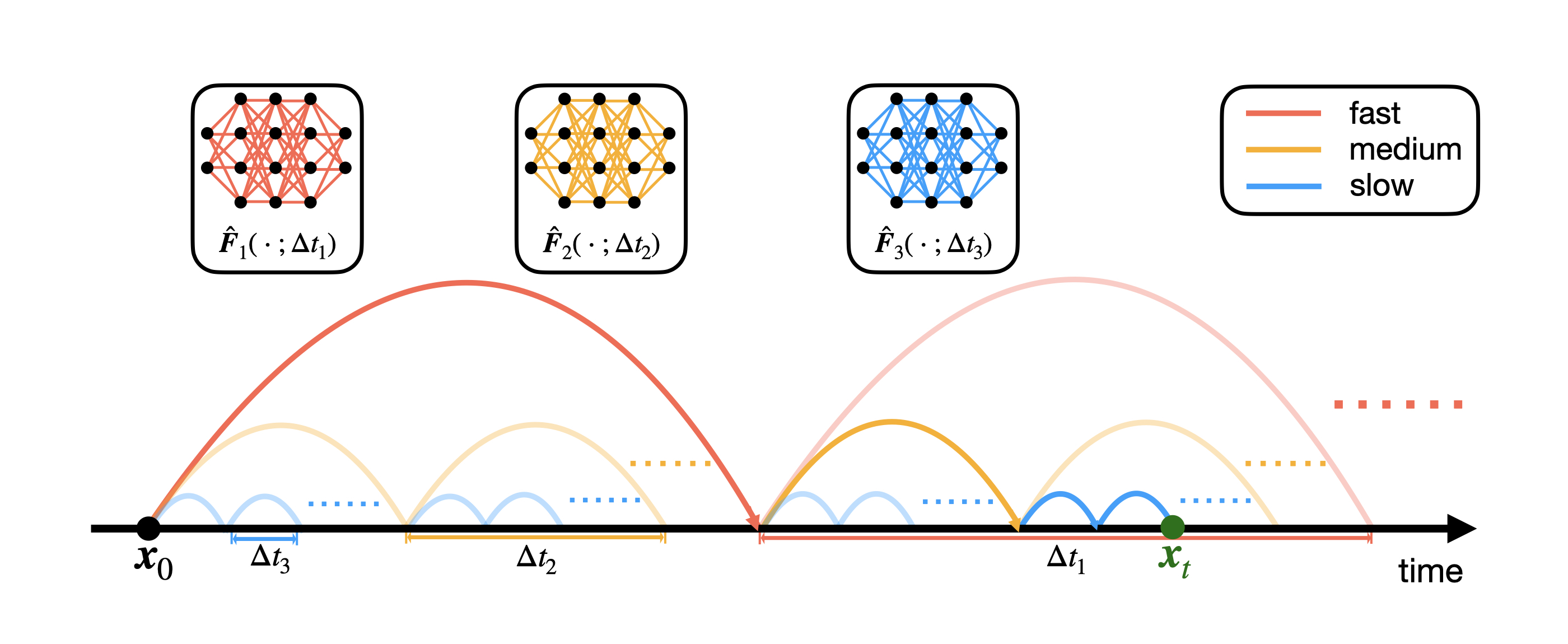
Nonlinear differential equations rarely admit closed-form solutions, thus requiring numerical time-stepping algorithms to approximate solutions. Further, many systems characterized by multiscale physics exhibit dynamics over a vast range of timescales, making numerical integration computationally expensive due to numerical stiffness. In this work, we develop a hierarchy of deep neural network time-steppers to approximate the flow map of the dynamical system over a disparate range of time-scales. The resulting model is purely data-driven and leverages features of the multiscale dynamics, enabling numerical integration and forecasting that is both accurate and highly efficient. Moreover, similar ideas can be used to couple neural network-based models with classical numerical time-steppers. Our multiscale hierarchical time-stepping scheme provides important advantages over current time-stepping algorithms, including (i) circumventing numerical stiffness due to disparate time-scales, (ii) improved accuracy in comparison with leading neural-network architectures, (iii) efficiency in long-time simulation/forecasting due to explicit training of slow time-scale dynamics, and (iv) a flexible framework that is parallelizable and may be integrated with standard numerical time-stepping algorithms. The method is demonstrated on a wide range of nonlinear dynamical systems, including the Van der Pol oscillator, the Lorenz system, the Kuramoto-Sivashinsky equation, and fluid flow pass a cylinder; audio and video signals are also explored. On the sequence generation examples, we benchmark our algorithm against state-of-the-art methods, such as LSTM, reservoir computing, and clockwork RNN. Despite the structural simplicity of our method, it outperforms competing methods on numerical integration.
PDF Abstract