Towards Cross Domain Generalization of Hamiltonian Representation via Meta Learning
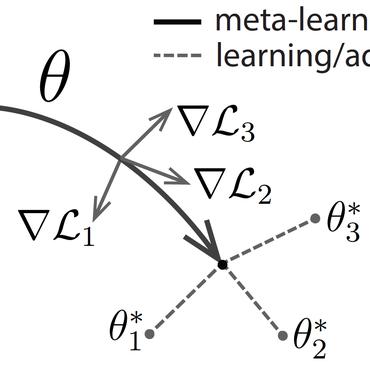
Recent advances in deep learning for physics have focused on discovering shared representations of target systems by incorporating physics priors or inductive biases into neural networks. While effective, these methods are limited to the system domain, where the type of system remains consistent and thus cannot ensure the adaptation to new, or unseen physical systems governed by different laws. For instance, a neural network trained on a mass-spring system cannot guarantee accurate predictions for the behavior of a two-body system or any other system with different physical laws. In this work, we take a significant leap forward by targeting cross domain generalization within the field of Hamiltonian dynamics. We model our system with a graph neural network and employ a meta learning algorithm to enable the model to gain experience over a distribution of tasks and make it adapt to new physics. Our approach aims to learn a unified Hamiltonian representation that is generalizable across multiple system domains, thereby overcoming the limitations of system-specific models. Our results demonstrate that the meta-trained model not only adapts effectively to new systems but also captures a generalized Hamiltonian representation that is consistent across different physical domains. Overall, through the use of meta learning, we offer a framework that achieves cross domain generalization, providing a step towards a unified model for understanding a wide array of dynamical systems via deep learning.
PDF Abstract