Optimal ridge penalty for real-world high-dimensional data can be zero or negative due to the implicit ridge regularization
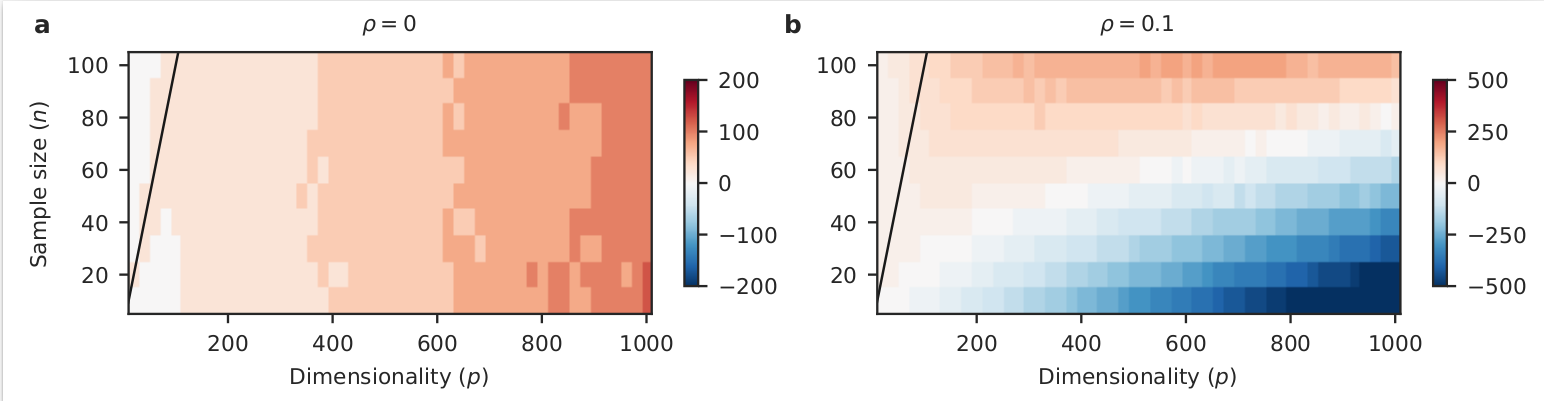
A conventional wisdom in statistical learning is that large models require strong regularization to prevent overfitting. Here we show that this rule can be violated by linear regression in the underdetermined $n\ll p$ situation under realistic conditions. Using simulations and real-life high-dimensional data sets, we demonstrate that an explicit positive ridge penalty can fail to provide any improvement over the minimum-norm least squares estimator. Moreover, the optimal value of ridge penalty in this situation can be negative. This happens when the high-variance directions in the predictor space can predict the response variable, which is often the case in the real-world high-dimensional data. In this regime, low-variance directions provide an implicit ridge regularization and can make any further positive ridge penalty detrimental. We prove that augmenting any linear model with random covariates and using minimum-norm estimator is asymptotically equivalent to adding the ridge penalty. We use a spiked covariance model as an analytically tractable example and prove that the optimal ridge penalty in this case is negative when $n\ll p$.
PDF Abstract