Interleaved Group Convolutions for Deep Neural Networks
In this paper, we present a simple and modularized neural network architecture, named interleaved group convolutional neural networks (IGCNets). The main point lies in a novel building block, a pair of two successive interleaved group convolutions: primary group convolution and secondary group convolution. The two group convolutions are complementary: (i) the convolution on each partition in primary group convolution is a spatial convolution, while on each partition in secondary group convolution, the convolution is a point-wise convolution; (ii) the channels in the same secondary partition come from different primary partitions. We discuss one representative advantage: Wider than a regular convolution with the number of parameters and the computation complexity preserved. We also show that regular convolutions, group convolution with summation fusion, and the Xception block are special cases of interleaved group convolutions. Empirical results over standard benchmarks, CIFAR-$10$, CIFAR-$100$, SVHN and ImageNet demonstrate that our networks are more efficient in using parameters and computation complexity with similar or higher accuracy.
PDF Abstract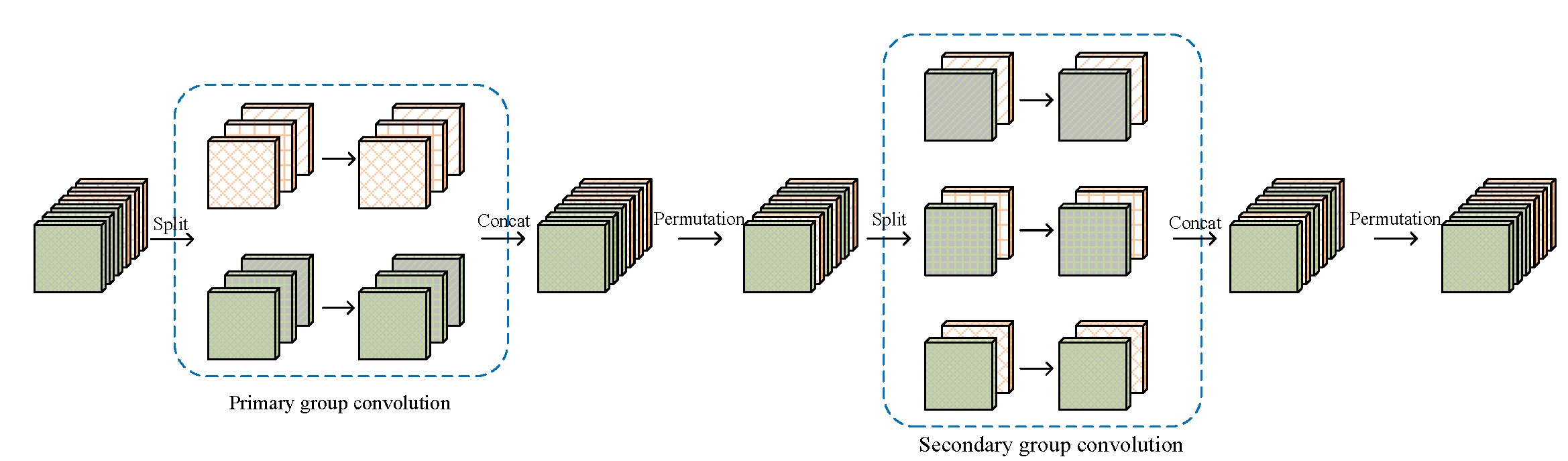

 CIFAR-10
CIFAR-10
 ImageNet
ImageNet
 CIFAR-100
CIFAR-100