$L_0$-ARM: Network Sparsification via Stochastic Binary Optimization
We consider network sparsification as an $L_0$-norm regularized binary optimization problem, where each unit of a neural network (e.g., weight, neuron, or channel, etc.) is attached with a stochastic binary gate, whose parameters are jointly optimized with original network parameters. The Augment-Reinforce-Merge (ARM), a recently proposed unbiased gradient estimator, is investigated for this binary optimization problem. Compared to the hard concrete gradient estimator from Louizos et al., ARM demonstrates superior performance of pruning network architectures while retaining almost the same accuracies of baseline methods. Similar to the hard concrete estimator, ARM also enables conditional computation during model training but with improved effectiveness due to the exact binary stochasticity. Thanks to the flexibility of ARM, many smooth or non-smooth parametric functions, such as scaled sigmoid or hard sigmoid, can be used to parameterize this binary optimization problem and the unbiasness of the ARM estimator is retained, while the hard concrete estimator has to rely on the hard sigmoid function to achieve conditional computation and thus accelerated training. Extensive experiments on multiple public datasets demonstrate state-of-the-art pruning rates with almost the same accuracies of baseline methods. The resulting algorithm $L_0$-ARM sparsifies the Wide-ResNet models on CIFAR-10 and CIFAR-100 while the hard concrete estimator cannot. The code is public available at https://github.com/leo-yangli/l0-arm.
PDF Abstract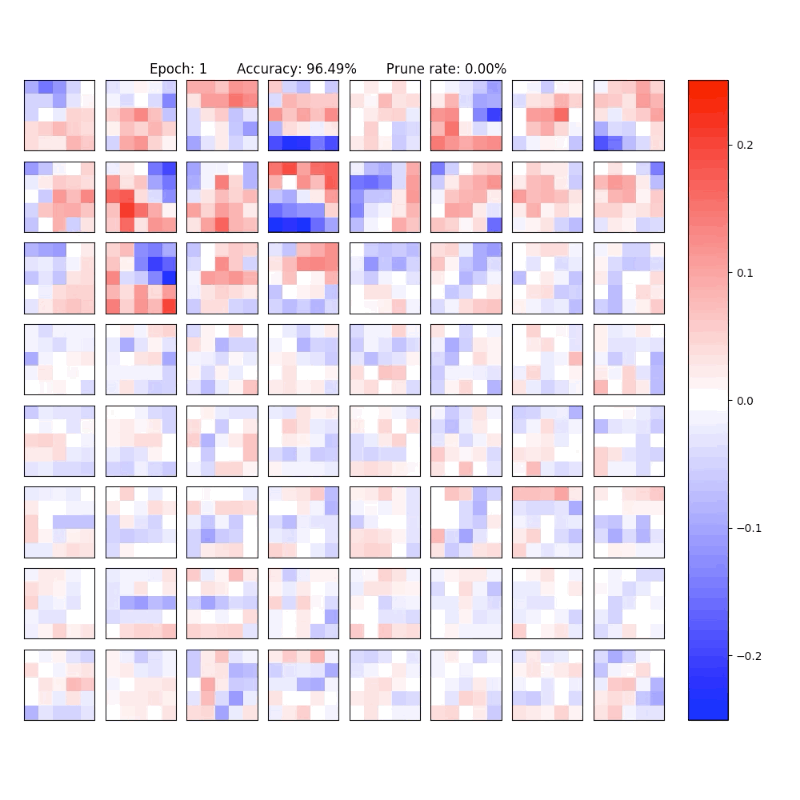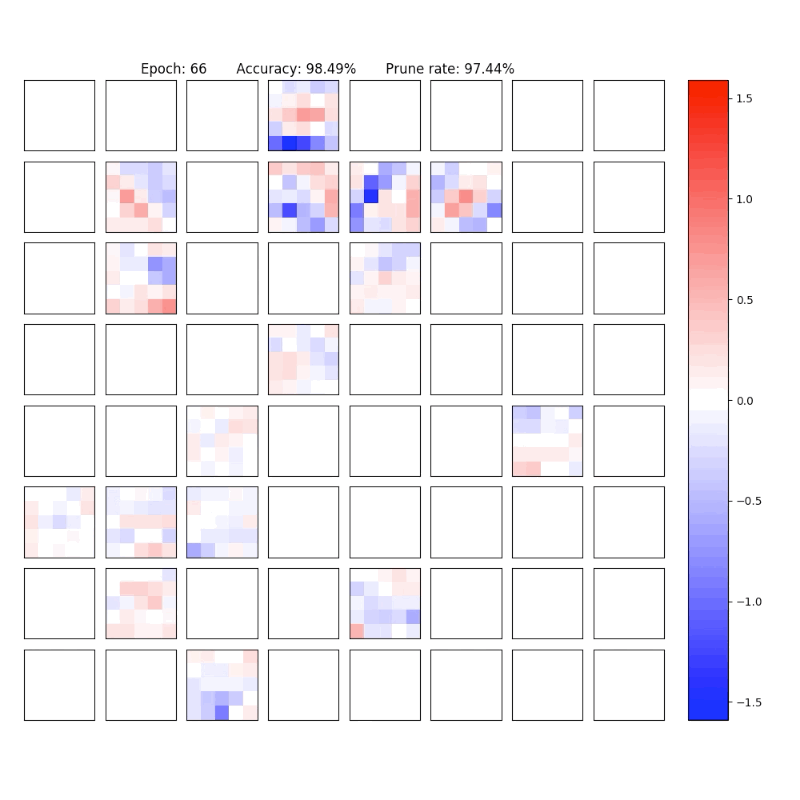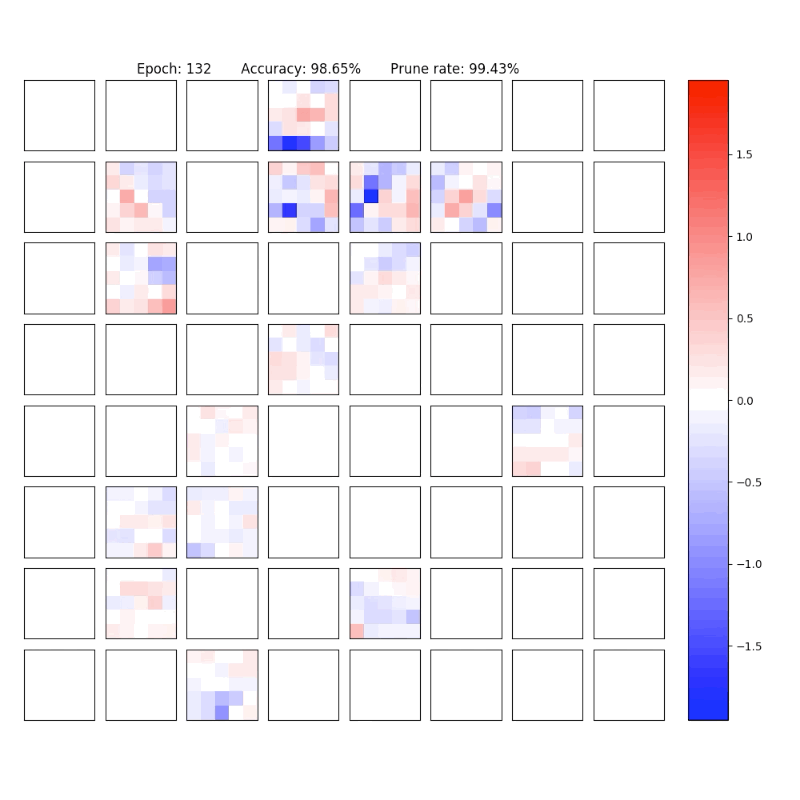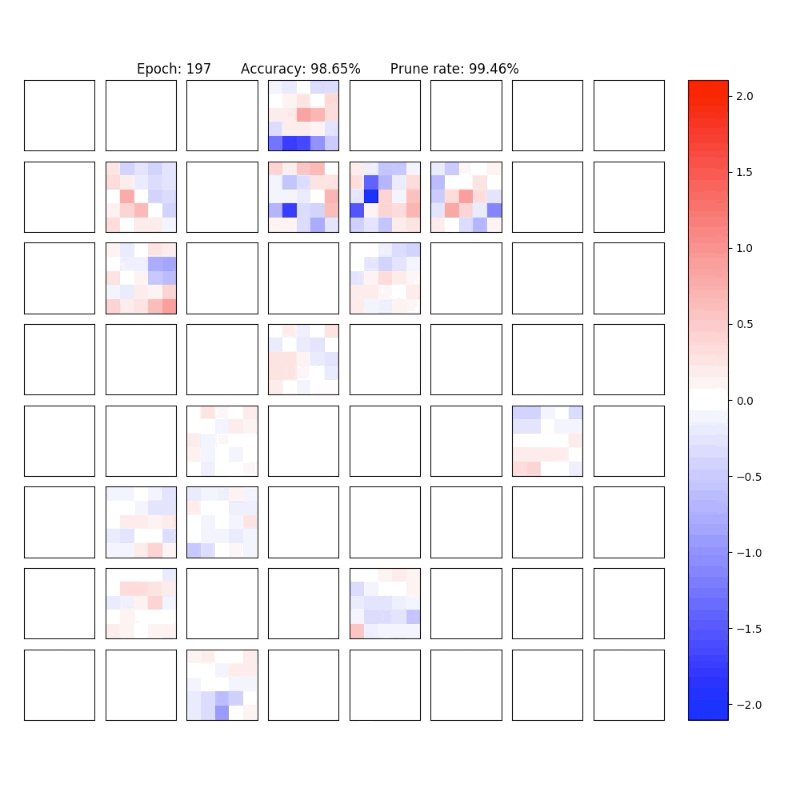

 CIFAR-10
CIFAR-10
 CIFAR-100
CIFAR-100
 MNIST
MNIST