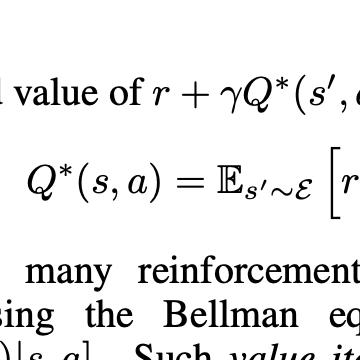Learning Gaussian Policies from Smoothed Action Value Functions
State-action value functions (i.e., Q-values) are ubiquitous in reinforcement learning (RL), giving rise to popular algorithms such as SARSA and Q-learning. We propose a new notion of action value defined by a Gaussian smoothed version of the expected Q-value used in SARSA. We show that such smoothed Q-values still satisfy a Bellman equation, making them naturally learnable from experience sampled from an environment. Moreover, the gradients of expected reward with respect to the mean and covariance of a parameterized Gaussian policy can be recovered from the gradient and Hessian of the smoothed Q-value function. Based on these relationships we develop new algorithms for training a Gaussian policy directly from a learned Q-value approximator. The approach is also amenable to proximal optimization techniques by augmenting the objective with a penalty on KL-divergence from a previous policy. We find that the ability to learn both a mean and covariance during training allows this approach to achieve strong results on standard continuous control benchmarks.
PDF Abstract