Is Nash Equilibrium Approximator Learnable?
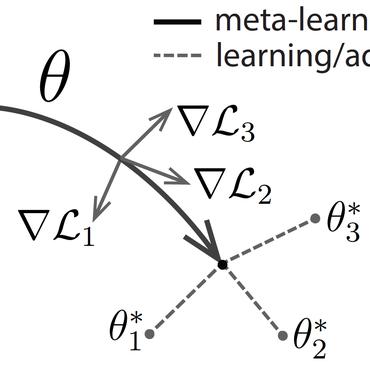
In this paper, we investigate the learnability of the function approximator that approximates Nash equilibrium (NE) for games generated from a distribution. First, we offer a generalization bound using the Probably Approximately Correct (PAC) learning model. The bound describes the gap between the expected loss and empirical loss of the NE approximator. Afterward, we prove the agnostic PAC learnability of the Nash approximator. In addition to theoretical analysis, we demonstrate an application of NE approximator in experiments. The trained NE approximator can be used to warm-start and accelerate classical NE solvers. Together, our results show the practicability of approximating NE through function approximation.
PDF Abstract
Datasets
Add Datasets
introduced or used in this paper
Results from the Paper
Submit
results from this paper
to get state-of-the-art GitHub badges and help the
community compare results to other papers.
Methods
No methods listed for this paper. Add
relevant methods here
