Linking Across Data Granularity: Fitting Multivariate Hawkes Processes to Partially Interval-Censored Data
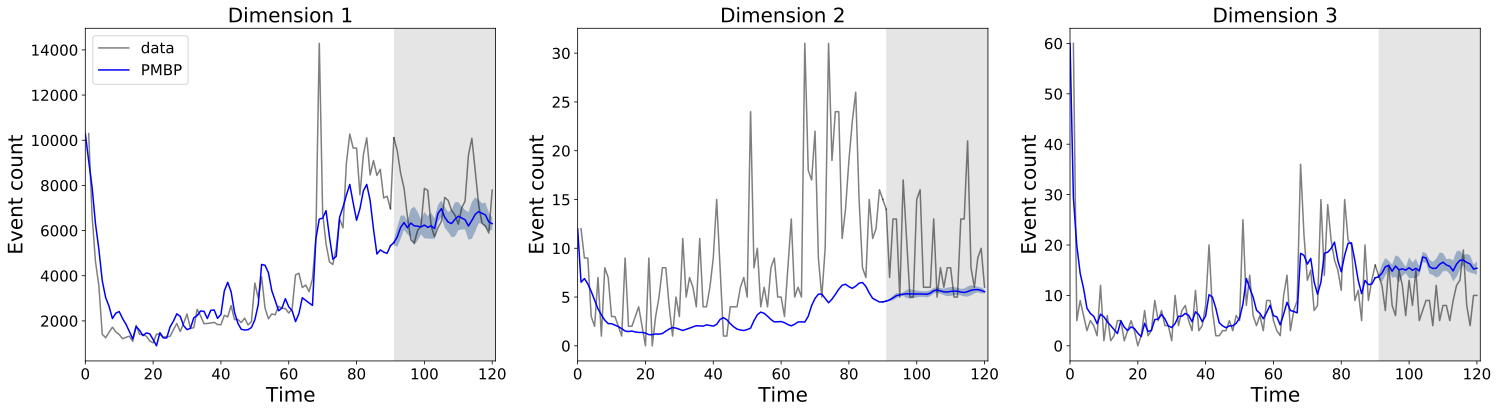
The multivariate Hawkes process (MHP) is widely used for analyzing data streams that interact with each other, where events generate new events within their own dimension (via self-excitation) or across different dimensions (via cross-excitation). However, in certain applications, the timestamps of individual events in some dimensions are unobservable, and only event counts within intervals are known, referred to as partially interval-censored data. The MHP is unsuitable for handling such data since its estimation requires event timestamps. In this study, we introduce the Partial Mean Behavior Poisson (PMBP) process, a novel point process which shares parameter equivalence with the MHP and can effectively model both timestamped and interval-censored data. We demonstrate the capabilities of the PMBP process using synthetic and real-world datasets. Firstly, we illustrate that the PMBP process can approximate MHP parameters and recover the spectral radius using synthetic event histories. Next, we assess the performance of the PMBP process in predicting YouTube popularity and find that it surpasses state-of-the-art methods. Lastly, we leverage the PMBP process to gain qualitative insights from a dataset comprising daily COVID-19 case counts from multiple countries and COVID-19-related news articles. By clustering the PMBP-modeled countries, we unveil hidden interaction patterns between occurrences of COVID-19 cases and news reporting.
PDF Abstract