Marginalizable Density Models
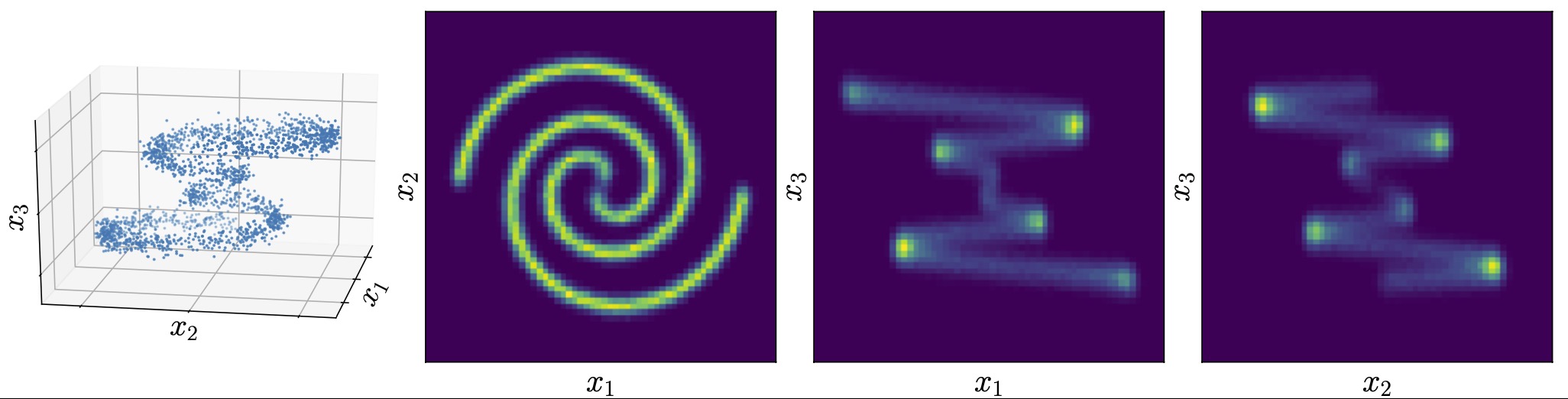
Probability density models based on deep networks have achieved remarkable success in modeling complex high-dimensional datasets. However, unlike kernel density estimators, modern neural models do not yield marginals or conditionals in closed form, as these quantities require the evaluation of seldom tractable integrals. In this work, we present the Marginalizable Density Model Approximator (MDMA), a novel deep network architecture which provides closed form expressions for the probabilities, marginals and conditionals of any subset of the variables. The MDMA learns deep scalar representations for each individual variable and combines them via learned hierarchical tensor decompositions into a tractable yet expressive CDF, from which marginals and conditional densities are easily obtained. We illustrate the advantage of exact marginalizability in several tasks that are out of reach of previous deep network-based density estimation models, such as estimating mutual information between arbitrary subsets of variables, inferring causality by testing for conditional independence, and inference with missing data without the need for data imputation, outperforming state-of-the-art models on these tasks. The model also allows for parallelized sampling with only a logarithmic dependence of the time complexity on the number of variables.
PDF Abstract