High-Dimensional Inference in Bayesian Networks
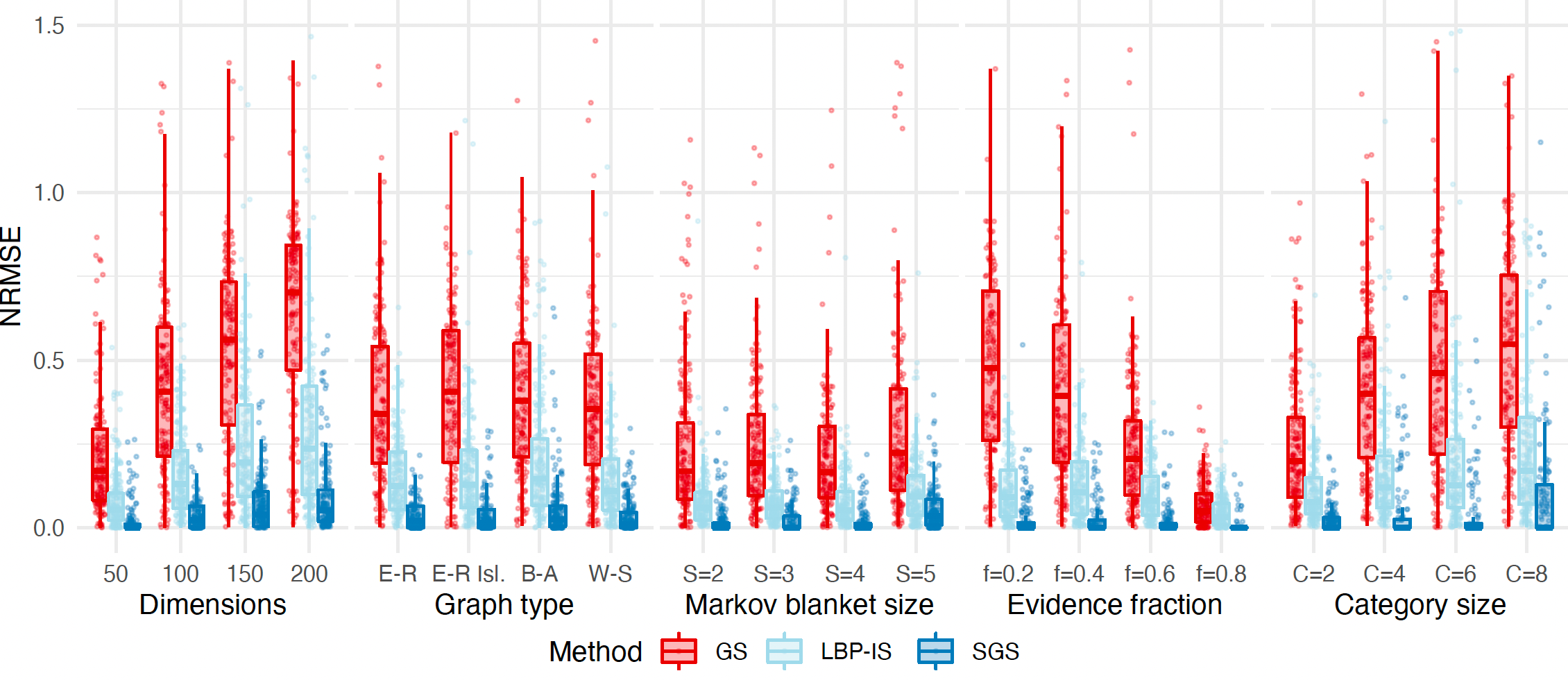
Inference of the marginal probability distribution is defined as the calculation of the probability of a subset of the variables and is relevant for handling missing data and hidden variables. While inference of the marginal probability distribution is crucial for various problems in machine learning and statistics, its exact computation is generally not feasible for categorical variables in Bayesian networks due to the NP-hardness of this task. We develop a divide-and-conquer approach using the graphical properties of Bayesian networks to split the computation of the marginal probability distribution into sub-calculations of lower dimensionality, thus reducing the overall computational complexity. Exploiting this property, we present an efficient and scalable algorithm for calculating the marginal probability distribution for categorical variables. The novel method is compared against state-of-the-art approximate inference methods in a benchmarking study, where it displays superior performance. As an immediate application, we demonstrate how our method can be used to classify incomplete data against Bayesian networks and use this approach for identifying the cancer subtype of kidney cancer patient samples.
PDF Abstract