Instrumental Variable Regression via Kernel Maximum Moment Loss
We investigate a simple objective for nonlinear instrumental variable (IV) regression based on a kernelized conditional moment restriction (CMR) known as a maximum moment restriction (MMR). The MMR objective is formulated by maximizing the interaction between the residual and the instruments belonging to a unit ball in a reproducing kernel Hilbert space (RKHS). First, it allows us to simplify the IV regression as an empirical risk minimization problem, where the risk functional depends on the reproducing kernel on the instrument and can be estimated by a U-statistic or V-statistic. Second, based on this simplification, we are able to provide the consistency and asymptotic normality results in both parametric and nonparametric settings. Lastly, we provide easy-to-use IV regression algorithms with an efficient hyper-parameter selection procedure. We demonstrate the effectiveness of our algorithms using experiments on both synthetic and real-world data.
PDF Abstract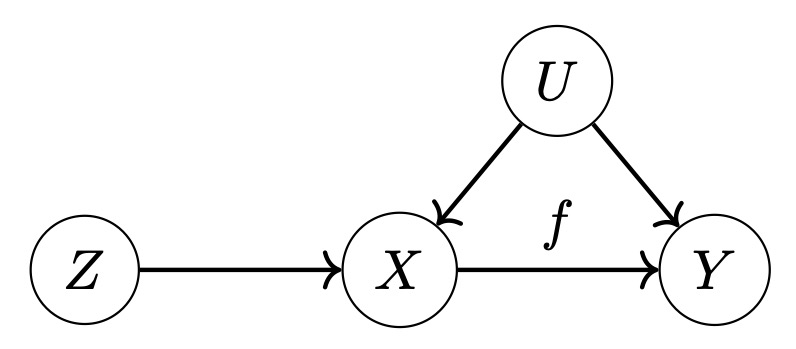


 MNIST
MNIST