Discovery of Multi-Level Network Differences Across Populations of Heterogeneous Connectomes
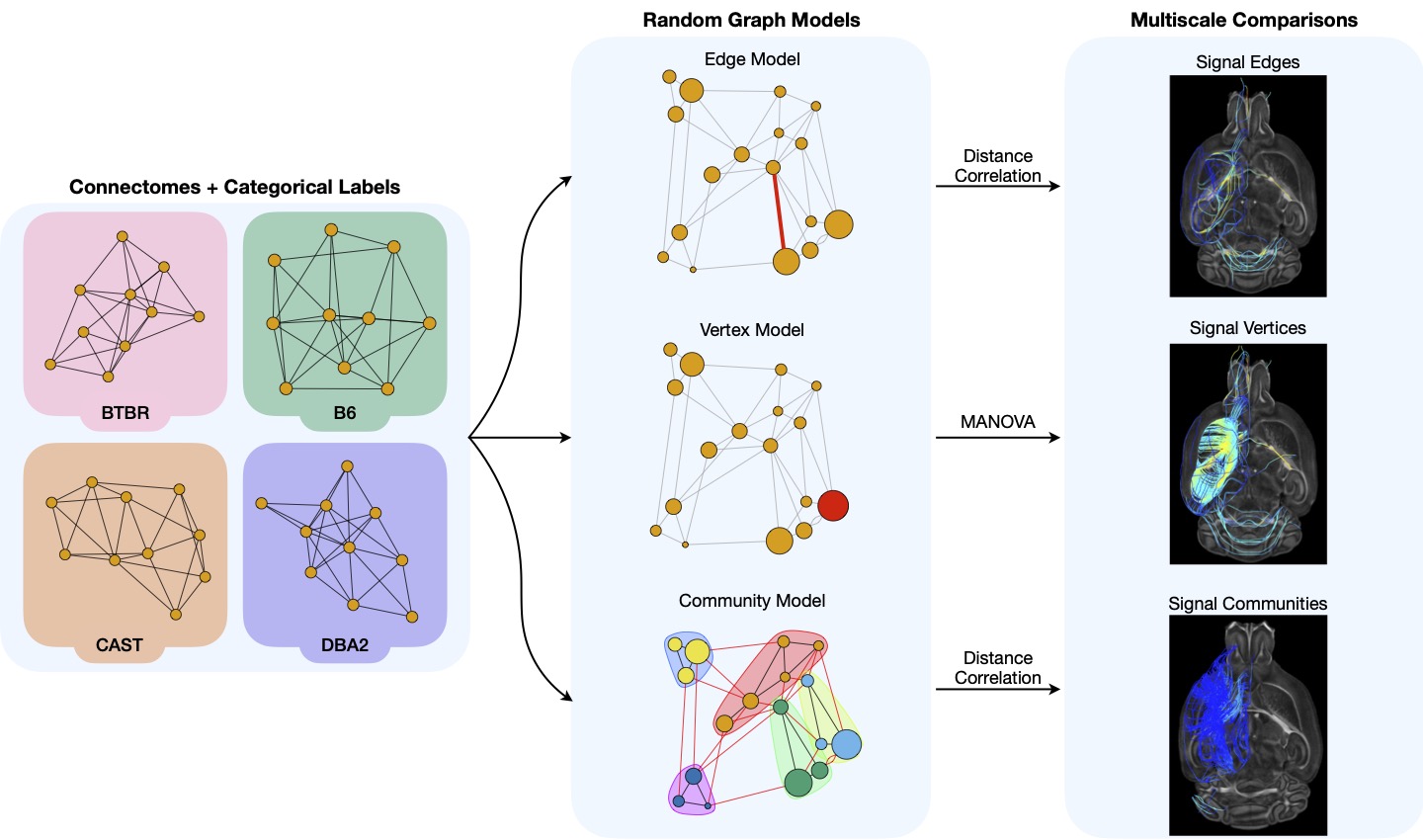
A connectome is a map of the structural and/or functional connections in the brain. This information-rich representation has the potential to transform our understanding of the relationship between patterns in brain connectivity and neurological processes, disorders, and diseases. However, existing computational techniques used to analyze connectomes are oftentimes insufficient for interrogating multi-subject connectomics datasets: most current methods are either solely designed to analyze single connectomes, or leverage heuristic graph statistics that are unable to capture the complete topology of connections between brain regions. To enable more rigorous connectomics analysis, we introduce a set of robust and interpretable statistical hypothesis tests motivated by recent theoretical advances in random graph models. These tests facilitate simultaneous analysis of multiple connectomes across different levels of network topology, enabling the robust and reproducible discovery of hierarchical brain structures that vary in relation with phenotypic profiles. In addition to explaining the theoretical foundations and guarantees of our hypothesis tests, we demonstrate their superiority over current state-of-the-art connectomics methods through extensive simulation studies, as well as synthetic and real-data experiments. Using a set of high-resolution connectomes obtained from genetically distinct mouse strains (including the BTBR mouse -- a standard model of autism -- and three behavioral wild-types), we illustrate how our methods can be used to successfully uncover latent information in multi-subject connectomics data and yield valuable insights into the connective correlates of neurological phenotypes. The code necessary to reproduce the analyses, simulations, and figures presented in this work are available in a series of Jupyter Notebooks (https://github.com/neurodata/MCC).
PDF Abstract