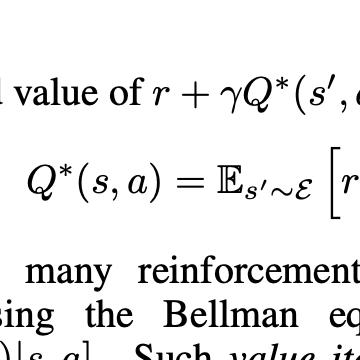No-Regret Reinforcement Learning with Heavy-Tailed Rewards
Reinforcement learning algorithms typically assume rewards to be sampled from light-tailed distributions, such as Gaussian or bounded. However, a wide variety of real-world systems generate rewards that follow heavy-tailed distributions. We consider such scenarios in the setting of undiscounted reinforcement learning. By constructing a lower bound, we show that the difficulty of learning heavy-tailed rewards asymptotically dominates the difficulty of learning transition probabilities. Leveraging techniques from robust mean estimation, we propose Heavy-UCRL2 and Heavy-Q-Learning, and show that they achieve near-optimal regret bounds in this setting. Our algorithms also naturally generalize to deep reinforcement learning applications; we instantiate Heavy-DQN as an example of this. We demonstrate that all of our algorithms outperform baselines on both synthetic MDPs and standard RL benchmarks.
PDF Abstract