Norm-in-Norm Loss with Faster Convergence and Better Performance for Image Quality Assessment
Currently, most image quality assessment (IQA) models are supervised by the MAE or MSE loss with empirically slow convergence. It is well-known that normalization can facilitate fast convergence. Therefore, we explore normalization in the design of loss functions for IQA. Specifically, we first normalize the predicted quality scores and the corresponding subjective quality scores. Then, the loss is defined based on the norm of the differences between these normalized values. The resulting "Norm-in-Norm'' loss encourages the IQA model to make linear predictions with respect to subjective quality scores. After training, the least squares regression is applied to determine the linear mapping from the predicted quality to the subjective quality. It is shown that the new loss is closely connected with two common IQA performance criteria (PLCC and RMSE). Through theoretical analysis, it is proved that the embedded normalization makes the gradients of the loss function more stable and more predictable, which is conducive to the faster convergence of the IQA model. Furthermore, to experimentally verify the effectiveness of the proposed loss, it is applied to solve a challenging problem: quality assessment of in-the-wild images. Experiments on two relevant datasets (KonIQ-10k and CLIVE) show that, compared to MAE or MSE loss, the new loss enables the IQA model to converge about 10 times faster and the final model achieves better performance. The proposed model also achieves state-of-the-art prediction performance on this challenging problem. For reproducible scientific research, our code is publicly available at https://github.com/lidq92/LinearityIQA.
PDF Abstract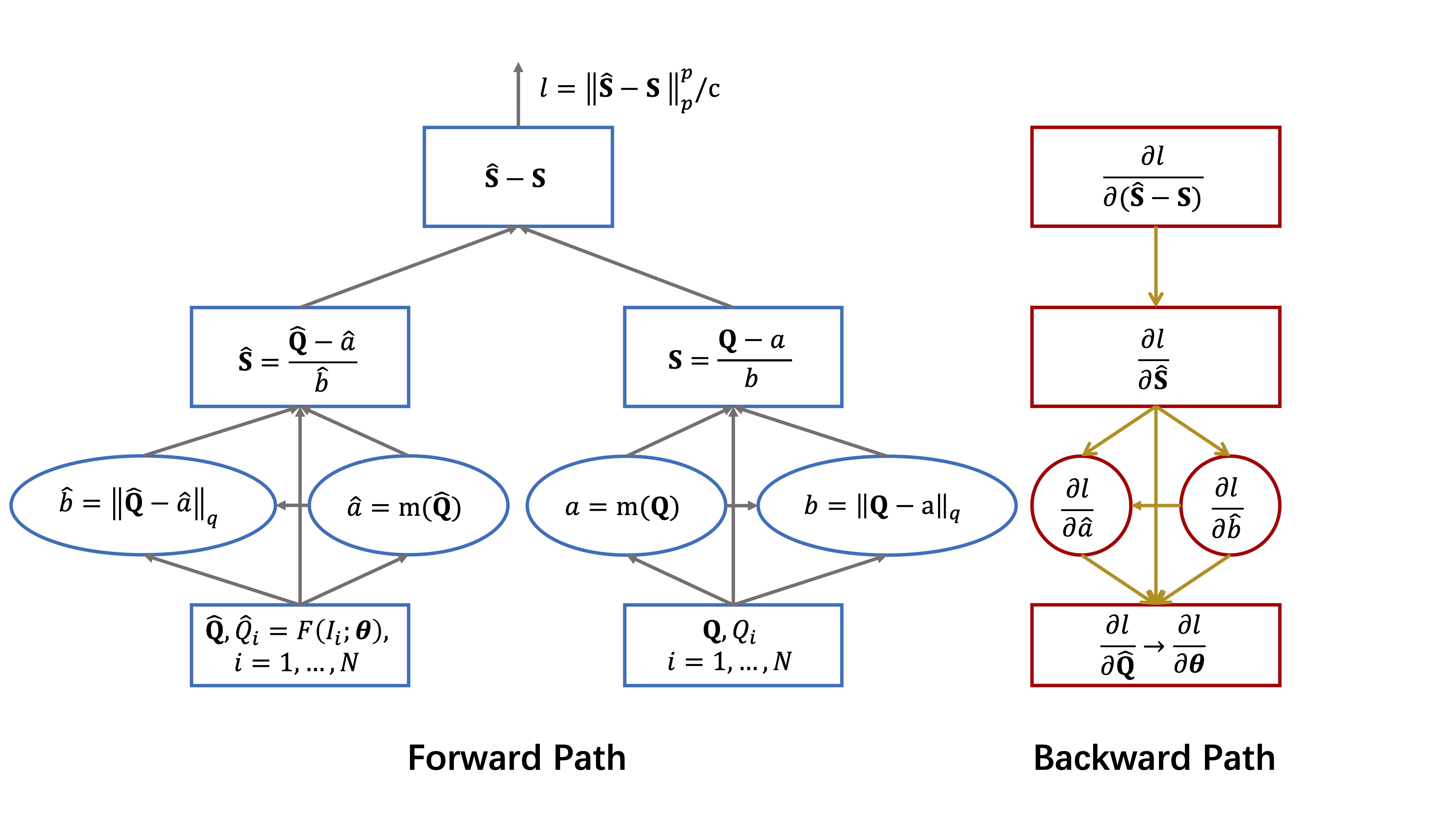






 KonIQ-10k
KonIQ-10k
 MSU NR VQA Database
MSU NR VQA Database
