Composite Q-learning: Multi-scale Q-function Decomposition and Separable Optimization
In the past few years, off-policy reinforcement learning methods have shown promising results in their application for robot control. Deep Q-learning, however, still suffers from poor data-efficiency and is susceptible to stochasticity in the environment or reward functions which is limiting with regard to real-world applications. We alleviate these problems by proposing two novel off-policy Temporal-Difference formulations: (1) Truncated Q-functions which represent the return for the first n steps of a target-policy rollout w.r.t. the full action-value and (2) Shifted Q-functions, acting as the farsighted return after this truncated rollout. This decomposition allows us to optimize both parts with their individual learning rates, achieving significant learning speedup. We prove that the combination of these short- and long-term predictions is a representation of the full return, leading to the Composite Q-learning algorithm. We show the efficacy of Composite Q-learning in the tabular case and compare Deep Composite Q-learning with TD3 and TD3(Delta), which we introduce as an off-policy variant of TD(Delta). Moreover, we show that Composite TD3 outperforms TD3 as well as state-of-the-art compositional Q-learning approaches significantly in terms of data-efficiency in multiple simulated robot tasks and that Composite Q-learning is robust to stochastic environments and reward functions.
PDF Abstract
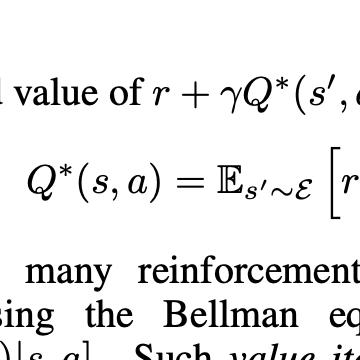
 MuJoCo
MuJoCo