On the Subspace Structure of Gradient-Based Meta-Learning
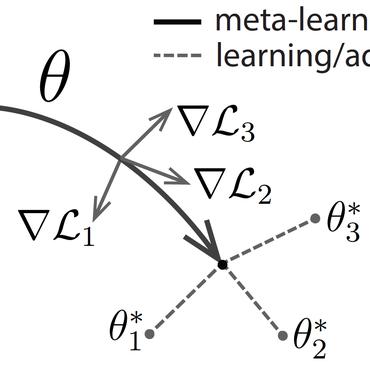
In this work we provide an analysis of the distribution of the post-adaptation parameters of Gradient-Based Meta-Learning (GBML) methods. Previous work has noticed how, for the case of image-classification, this adaptation only takes place on the last layers of the network. We propose the more general notion that parameters are updated over a low-dimensional \emph{subspace} of the same dimensionality as the task-space and show that this holds for regression as well. Furthermore, the induced subspace structure provides a method to estimate the intrinsic dimension of the space of tasks of common few-shot learning datasets.
PDF Abstract
Datasets
Results from the Paper
Submit
results from this paper
to get state-of-the-art GitHub badges and help the
community compare results to other papers.
Methods
No methods listed for this paper. Add
relevant methods here
