Optimal Transport for structured data with application on graphs
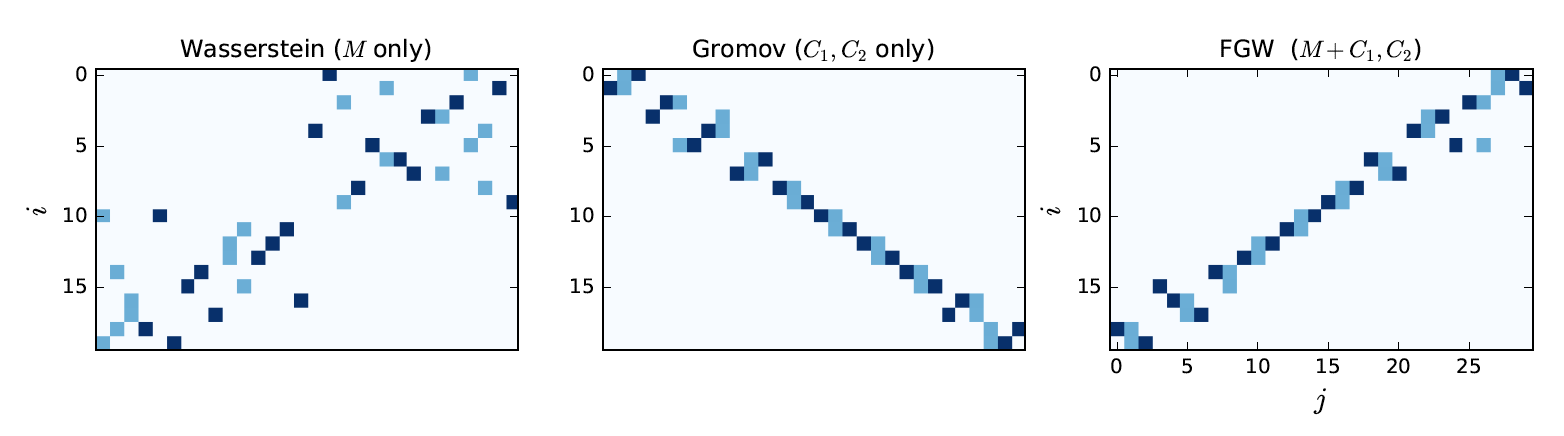
This work considers the problem of computing distances between structured objects such as undirected graphs, seen as probability distributions in a specific metric space. We consider a new transportation distance (i.e. that minimizes a total cost of transporting probability masses) that unveils the geometric nature of the structured objects space. Unlike Wasserstein or Gromov-Wasserstein metrics that focus solely and respectively on features (by considering a metric in the feature space) or structure (by seeing structure as a metric space), our new distance exploits jointly both information, and is consequently called Fused Gromov-Wasserstein (FGW). After discussing its properties and computational aspects, we show results on a graph classification task, where our method outperforms both graph kernels and deep graph convolutional networks. Exploiting further on the metric properties of FGW, interesting geometric objects such as Fr\'echet means or barycenters of graphs are illustrated and discussed in a clustering context.
PDF Abstract