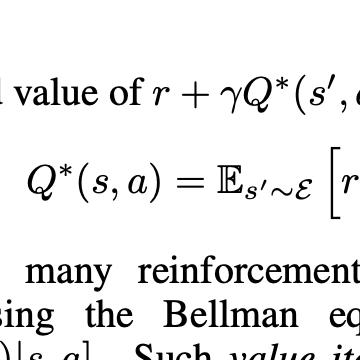Optimal variance-reduced stochastic approximation in Banach spaces
We study the problem of estimating the fixed point of a contractive operator defined on a separable Banach space. Focusing on a stochastic query model that provides noisy evaluations of the operator, we analyze a variance-reduced stochastic approximation scheme, and establish non-asymptotic bounds for both the operator defect and the estimation error, measured in an arbitrary semi-norm. In contrast to worst-case guarantees, our bounds are instance-dependent, and achieve the local asymptotic minimax risk non-asymptotically. For linear operators, contractivity can be relaxed to multi-step contractivity, so that the theory can be applied to problems like average reward policy evaluation problem in reinforcement learning. We illustrate the theory via applications to stochastic shortest path problems, two-player zero-sum Markov games, as well as policy evaluation and $Q$-learning for tabular Markov decision processes.
PDF Abstract