Parallax: Visualizing and Understanding the Semantics of Embedding Spaces via Algebraic Formulae
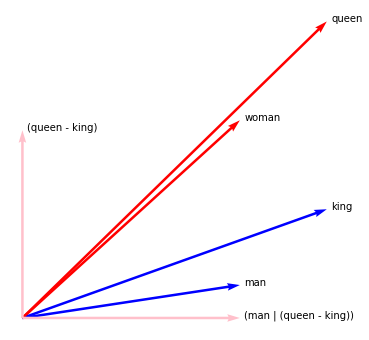
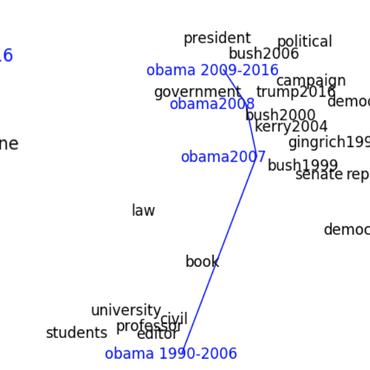
Embeddings are a fundamental component of many modern machine learning and natural language processing models. Understanding them and visualizing them is essential for gathering insights about the information they capture and the behavior of the models. State of the art in analyzing embeddings consists in projecting them in two-dimensional planes without any interpretable semantics associated to the axes of the projection, which makes detailed analyses and comparison among multiple sets of embeddings challenging. In this work, we propose to use explicit axes defined as algebraic formulae over embeddings to project them into a lower dimensional, but semantically meaningful subspace, as a simple yet effective analysis and visualization methodology. This methodology assigns an interpretable semantics to the measures of variability and the axes of visualizations, allowing for both comparisons among different sets of embeddings and fine-grained inspection of the embedding spaces. We demonstrate the power of the proposed methodology through a series of case studies that make use of visualizations constructed around the underlying methodology and through a user study. The results show how the methodology is effective at providing more profound insights than classical projection methods and how it is widely applicable to many other use cases.
PDF Abstract ACL 2019 PDF ACL 2019 Abstract