Poisson Flow Generative Models
We propose a new "Poisson flow" generative model (PFGM) that maps a uniform distribution on a high-dimensional hemisphere into any data distribution. We interpret the data points as electrical charges on the $z=0$ hyperplane in a space augmented with an additional dimension $z$, generating a high-dimensional electric field (the gradient of the solution to Poisson equation). We prove that if these charges flow upward along electric field lines, their initial distribution in the $z=0$ plane transforms into a distribution on the hemisphere of radius $r$ that becomes uniform in the $r \to\infty$ limit. To learn the bijective transformation, we estimate the normalized field in the augmented space. For sampling, we devise a backward ODE that is anchored by the physically meaningful additional dimension: the samples hit the unaugmented data manifold when the $z$ reaches zero. Experimentally, PFGM achieves current state-of-the-art performance among the normalizing flow models on CIFAR-10, with an Inception score of $9.68$ and a FID score of $2.35$. It also performs on par with the state-of-the-art SDE approaches while offering $10\times $ to $20 \times$ acceleration on image generation tasks. Additionally, PFGM appears more tolerant of estimation errors on a weaker network architecture and robust to the step size in the Euler method. The code is available at https://github.com/Newbeeer/poisson_flow .
PDF Abstract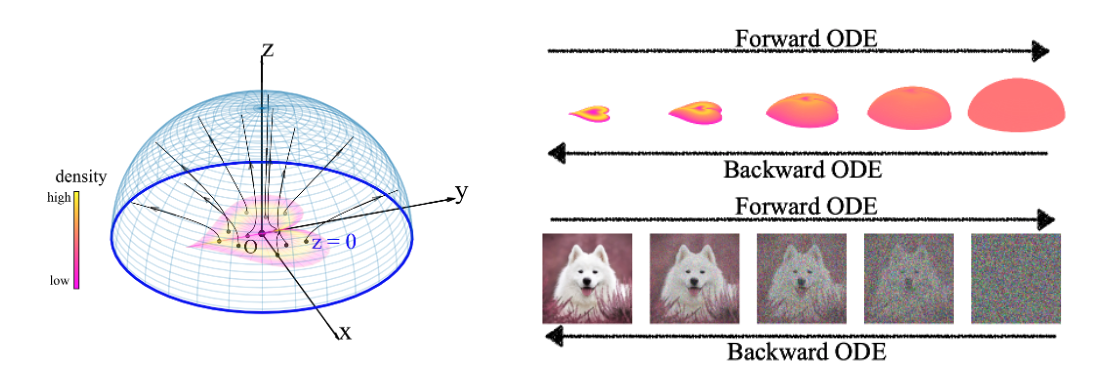



 CIFAR-10
CIFAR-10
 LSUN
LSUN
