Practical and scalable simulations of non-Markovian stochastic processes
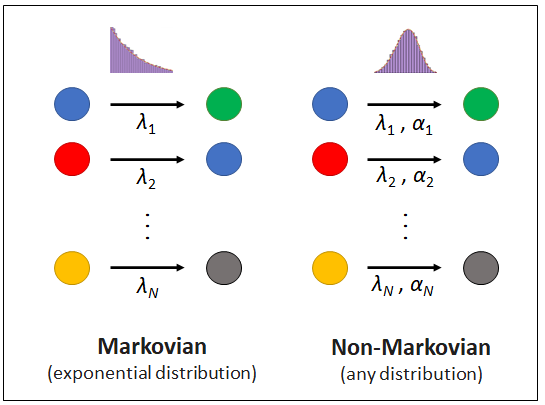
Discrete stochastic processes are widespread in natural systems with many applications across physics, biochemistry, epidemiology, sociology, and finance. While analytic solutions often cannot be derived, existing simulation frameworks can generate stochastic trajectories compatible with the dynamical laws underlying the random phenomena. However, most simulation algorithms assume the system dynamics are memoryless (Markovian assumption), under which assumption, future occurrences only depend on the present state of the system. Mathematically, the Markovian assumption models inter-event times as exponentially distributed variables, which enables the exact simulation of stochastic trajectories using the seminal Gillespie algorithm. Unfortunately, the majority of stochastic systems exhibit properties of memory, an inherently non-Markovian attribute. Non-Markovian systems are notoriously difficult to investigate analytically, and existing numerical methods are computationally costly or only applicable under strong simplifying assumptions, often not compatible with empirical observations. To address these challenges, we have developed the Rejection-based Gillespie algorithm for non-Markovian Reactions (REGIR), a general and scalable framework to simulate non-Markovian stochastic systems with arbitrary inter-event time distributions. REGIR can achieve arbitrary user-defined accuracy while maintaining the same asymptotic computational complexity as the Gillespie algorithm. We illustrate REGIR's modeling capabilities in three important biochemical systems, namely microbial growth dynamics, stem cell differentiation, and RNA transcription. In all three cases, REGIR efficiently models the underlying stochastic processes and demonstrates its utility to accurately investigate complex non-Markovian systems. The algorithm is implemented as a python library REGIR.
PDF Abstract