Provable defenses against adversarial examples via the convex outer adversarial polytope
We propose a method to learn deep ReLU-based classifiers that are provably robust against norm-bounded adversarial perturbations on the training data. For previously unseen examples, the approach is guaranteed to detect all adversarial examples, though it may flag some non-adversarial examples as well. The basic idea is to consider a convex outer approximation of the set of activations reachable through a norm-bounded perturbation, and we develop a robust optimization procedure that minimizes the worst case loss over this outer region (via a linear program). Crucially, we show that the dual problem to this linear program can be represented itself as a deep network similar to the backpropagation network, leading to very efficient optimization approaches that produce guaranteed bounds on the robust loss. The end result is that by executing a few more forward and backward passes through a slightly modified version of the original network (though possibly with much larger batch sizes), we can learn a classifier that is provably robust to any norm-bounded adversarial attack. We illustrate the approach on a number of tasks to train classifiers with robust adversarial guarantees (e.g. for MNIST, we produce a convolutional classifier that provably has less than 5.8% test error for any adversarial attack with bounded $\ell_\infty$ norm less than $\epsilon = 0.1$), and code for all experiments in the paper is available at https://github.com/locuslab/convex_adversarial.
PDF Abstract ICML 2018 PDF ICML 2018 Abstract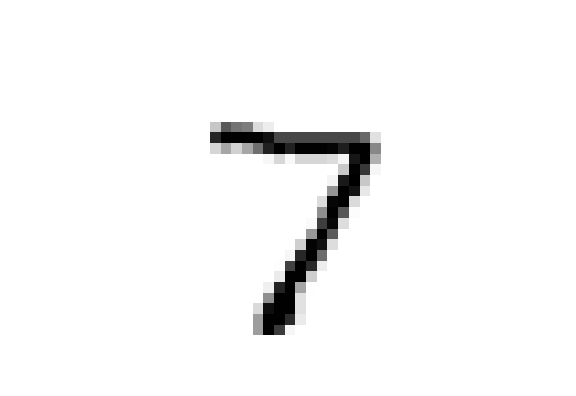


 Fashion-MNIST
Fashion-MNIST
 HAR
HAR