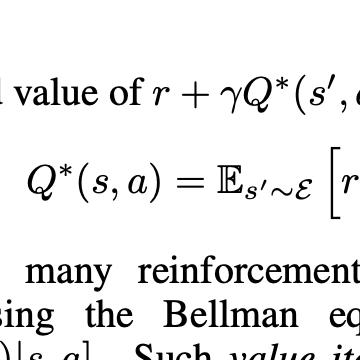Provably Efficient Reinforcement Learning with Aggregated States
We establish that an optimistic variant of Q-learning applied to a fixed-horizon episodic Markov decision process with an aggregated state representation incurs regret $\tilde{\mathcal{O}}(\sqrt{H^5 M K} + \epsilon HK)$, where $H$ is the horizon, $M$ is the number of aggregate states, $K$ is the number of episodes, and $\epsilon$ is the largest difference between any pair of optimal state-action values associated with a common aggregate state. Notably, this regret bound does not depend on the number of states or actions and indicates that asymptotic per-period regret is no greater than $\epsilon$, independent of horizon. To our knowledge, this is the first such result that applies to reinforcement learning with nontrivial value function approximation without any restrictions on transition probabilities.
PDF Abstract