Scalable Gradients for Stochastic Differential Equations
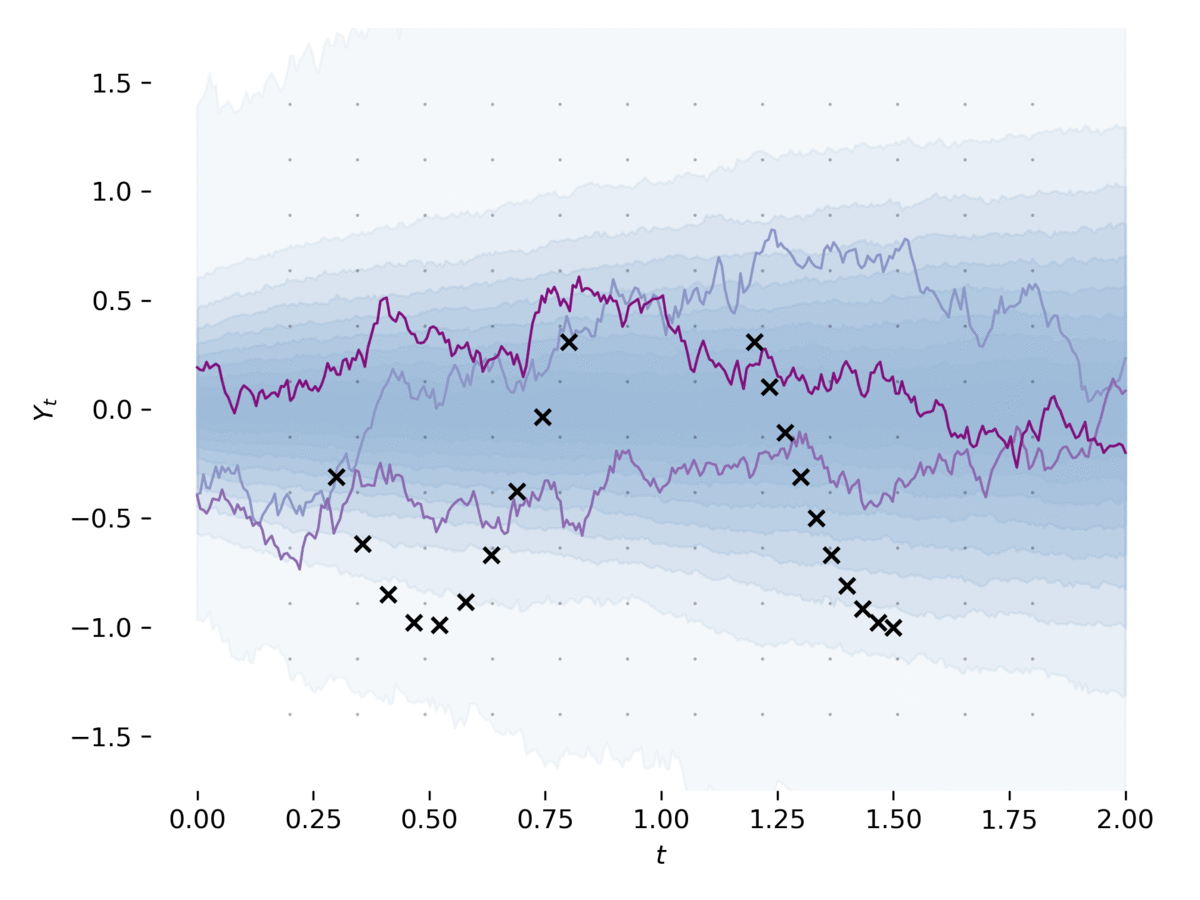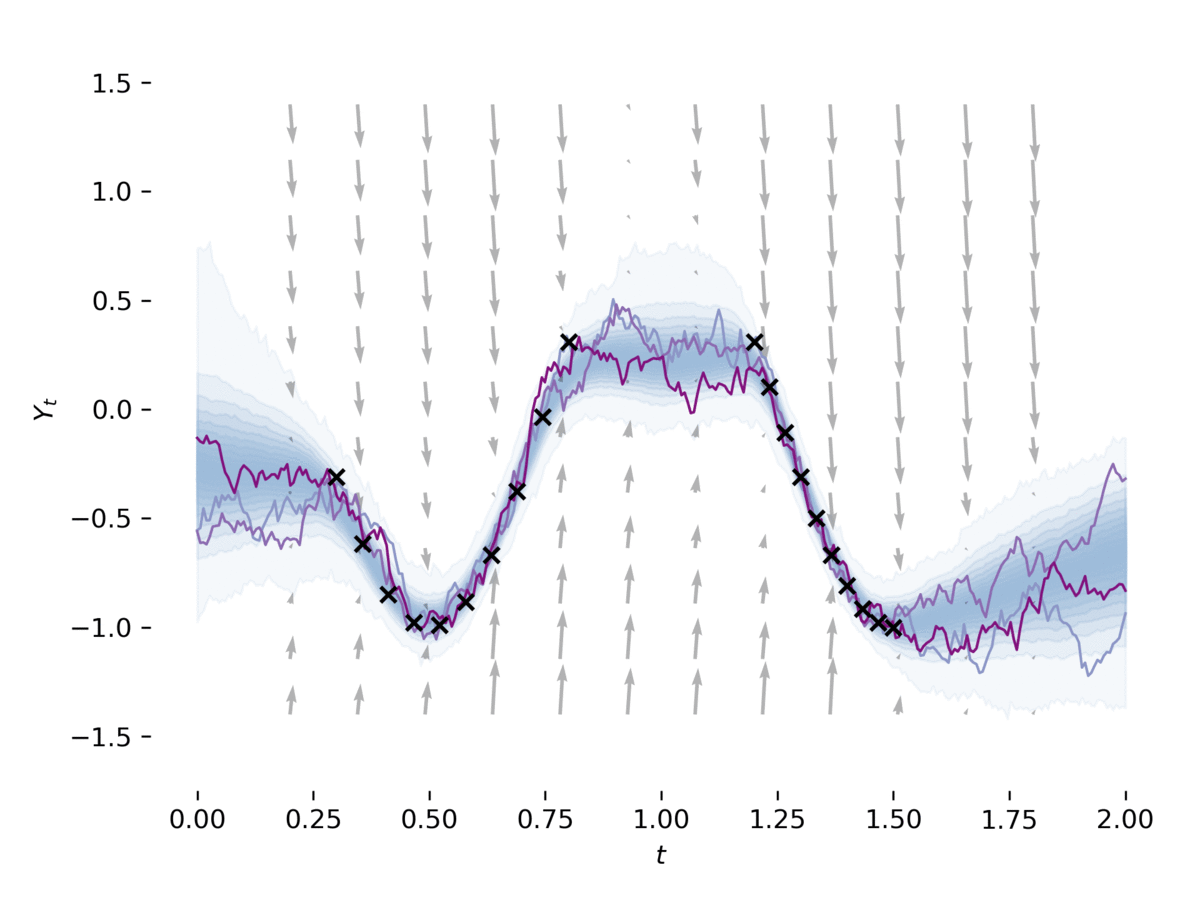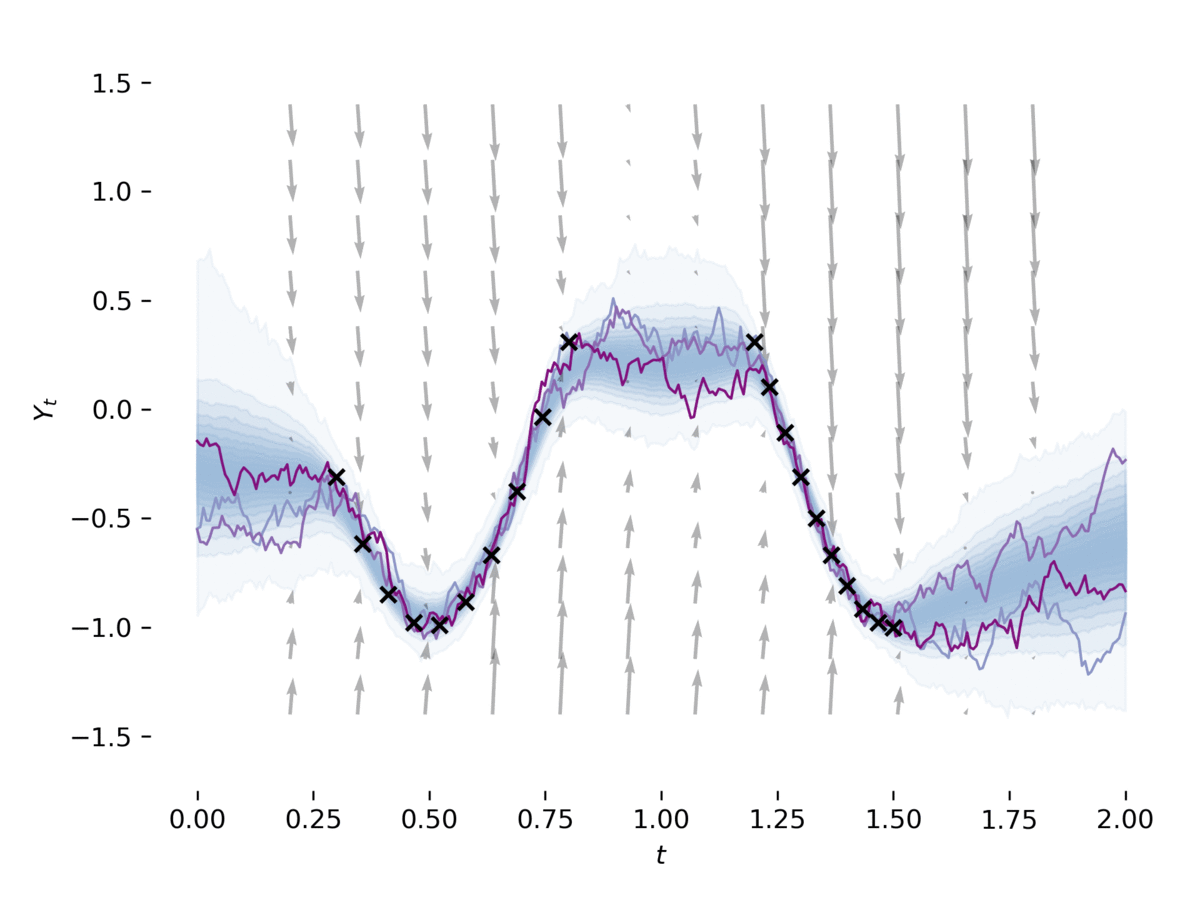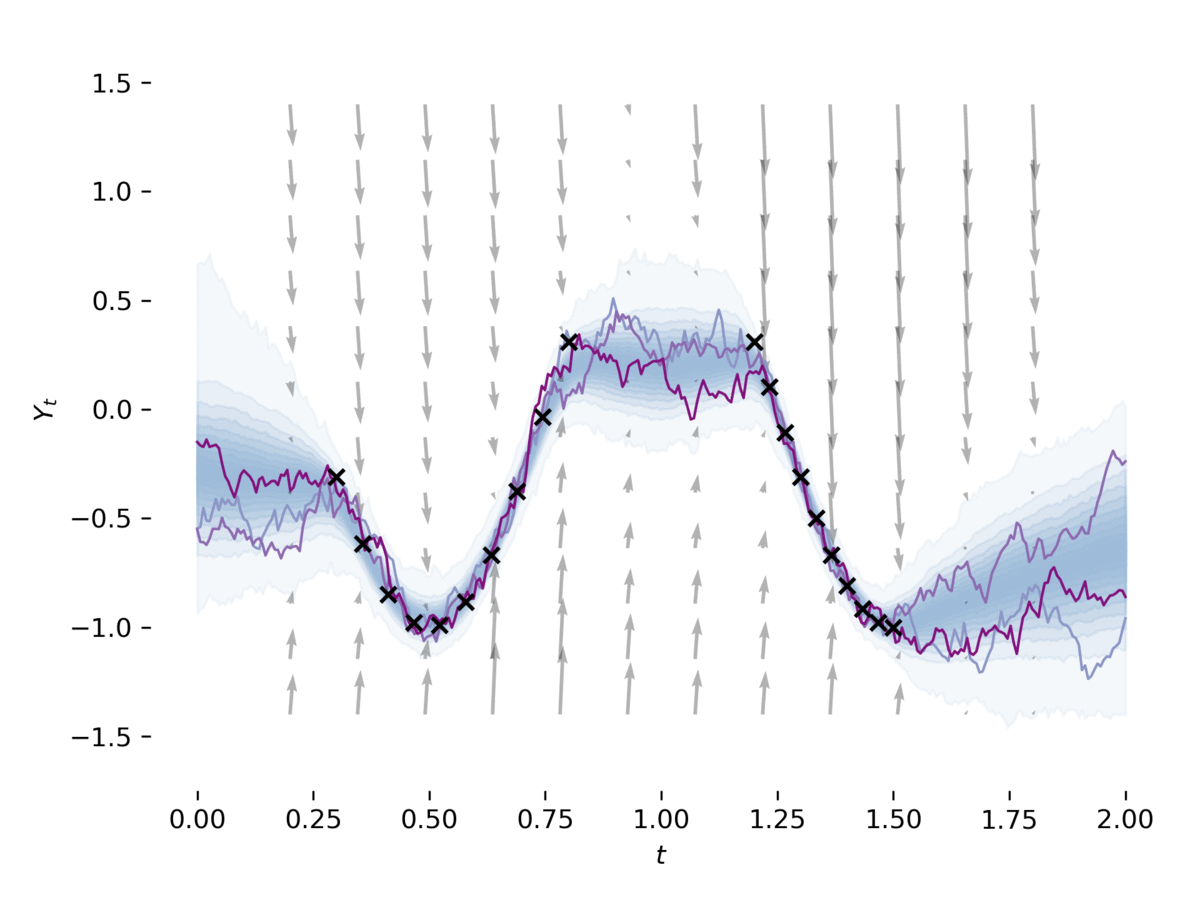
The adjoint sensitivity method scalably computes gradients of solutions to ordinary differential equations. We generalize this method to stochastic differential equations, allowing time-efficient and constant-memory computation of gradients with high-order adaptive solvers. Specifically, we derive a stochastic differential equation whose solution is the gradient, a memory-efficient algorithm for caching noise, and conditions under which numerical solutions converge. In addition, we combine our method with gradient-based stochastic variational inference for latent stochastic differential equations. We use our method to fit stochastic dynamics defined by neural networks, achieving competitive performance on a 50-dimensional motion capture dataset.
PDF Abstract