Structure-preserving neural networks
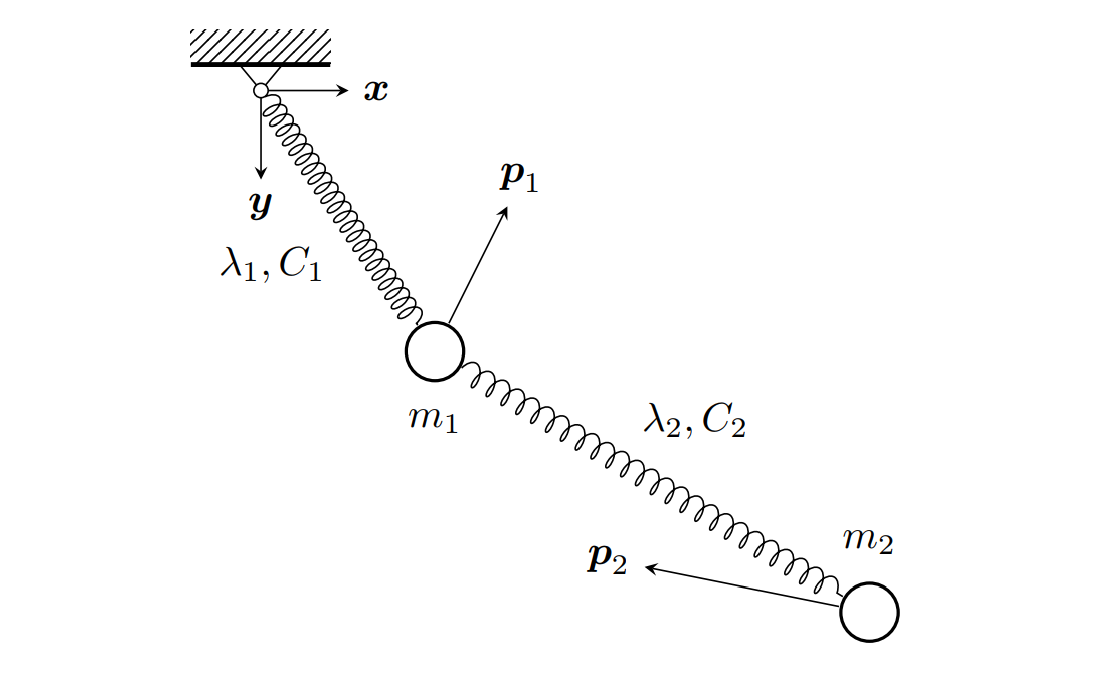
We develop a method to learn physical systems from data that employs feedforward neural networks and whose predictions comply with the first and second principles of thermodynamics. The method employs a minimum amount of data by enforcing the metriplectic structure of dissipative Hamiltonian systems in the form of the so-called General Equation for the Non-Equilibrium Reversible-Irreversible Coupling, GENERIC [M. Grmela and H.C Oettinger (1997). Dynamics and thermodynamics of complex fluids. I. Development of a general formalism. Phys. Rev. E. 56 (6): 6620-6632]. The method does not need to enforce any kind of balance equation, and thus no previous knowledge on the nature of the system is needed. Conservation of energy and dissipation of entropy in the prediction of previously unseen situations arise as a natural by-product of the structure of the method. Examples of the performance of the method are shown that include conservative as well as dissipative systems, discrete as well as continuous ones.
PDF Abstract