Dynamic Graph Convolutional Networks Using the Tensor M-Product
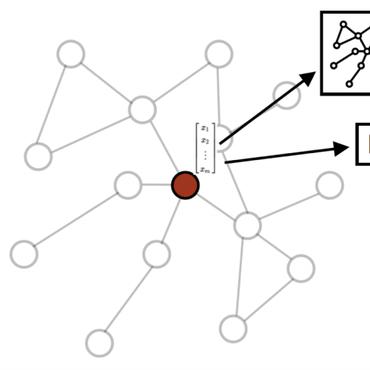
Many irregular domains such as social networks, financial transactions, neuron connections, and natural language constructs are represented using graph structures. In recent years, a variety of graph neural networks (GNNs) have been successfully applied for representation learning and prediction on such graphs. In many of the real-world applications, the underlying graph changes over time, however, most of the existing GNNs are inadequate for handling such dynamic graphs. In this paper we propose a novel technique for learning embeddings of dynamic graphs using a tensor algebra framework. Our method extends the popular graph convolutional network (GCN) for learning representations of dynamic graphs using the recently proposed tensor M-product technique. Theoretical results presented establish a connection between the proposed tensor approach and spectral convolution of tensors. The proposed method TM-GCN is consistent with the Message Passing Neural Network (MPNN) framework, accounting for both spatial and temporal message passing. Numerical experiments on real-world datasets demonstrate the performance of the proposed method for edge classification and link prediction tasks on dynamic graphs. We also consider an application related to the COVID-19 pandemic, and show how our method can be used for early detection of infected individuals from contact tracing data.
PDF Abstract ICLR 2020 PDF ICLR 2020 Abstract



 Reddit
Reddit