The general theory of permutation equivarant neural networks and higher order graph variational encoders
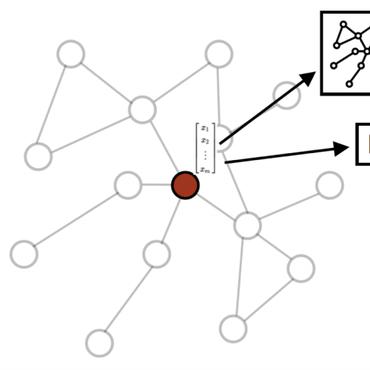
Previous work on symmetric group equivariant neural networks generally only considered the case where the group acts by permuting the elements of a single vector. In this paper we derive formulae for general permutation equivariant layers, including the case where the layer acts on matrices by permuting their rows and columns simultaneously. This case arises naturally in graph learning and relation learning applications. As a specific case of higher order permutation equivariant networks, we present a second order graph variational encoder, and show that the latent distribution of equivariant generative models must be exchangeable. We demonstrate the efficacy of this architecture on the tasks of link prediction in citation graphs and molecular graph generation.
PDF Abstract