Total Deep Variation: A Stable Regularizer for Inverse Problems
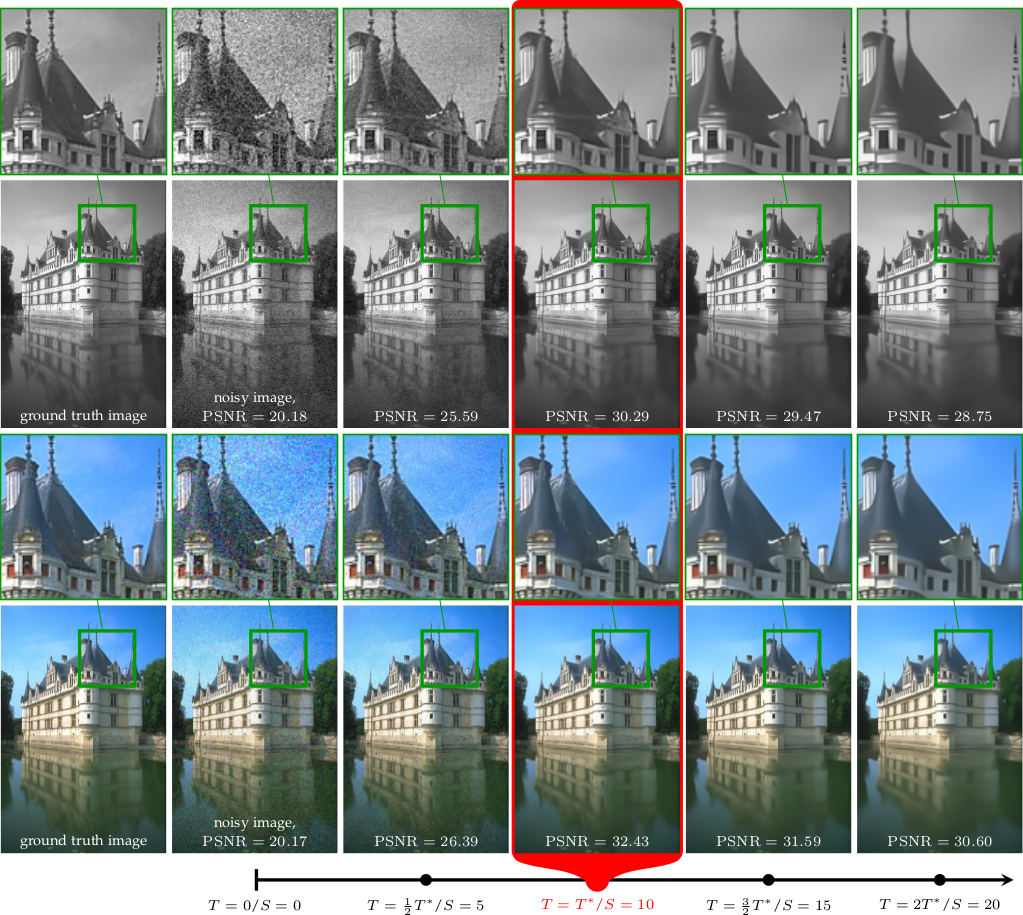
Various problems in computer vision and medical imaging can be cast as inverse problems. A frequent method for solving inverse problems is the variational approach, which amounts to minimizing an energy composed of a data fidelity term and a regularizer. Classically, handcrafted regularizers are used, which are commonly outperformed by state-of-the-art deep learning approaches. In this work, we combine the variational formulation of inverse problems with deep learning by introducing the data-driven general-purpose total deep variation regularizer. In its core, a convolutional neural network extracts local features on multiple scales and in successive blocks. This combination allows for a rigorous mathematical analysis including an optimal control formulation of the training problem in a mean-field setting and a stability analysis with respect to the initial values and the parameters of the regularizer. In addition, we experimentally verify the robustness against adversarial attacks and numerically derive upper bounds for the generalization error. Finally, we achieve state-of-the-art results for numerous imaging tasks.
PDF Abstract