On a Sparse Shortcut Topology of Artificial Neural Networks
In established network architectures, shortcut connections are often used to take the outputs of earlier layers as additional inputs to later layers. Despite the extraordinary effectiveness of shortcuts, there remain open questions on the mechanism and characteristics. For example, why are shortcuts powerful? Why do shortcuts generalize well? In this paper, we investigate the expressivity and generalizability of a novel sparse shortcut topology. First, we demonstrate that this topology can empower a one-neuron-wide deep network to approximate any univariate continuous function. Then, we present a novel width-bounded universal approximator in contrast to depth-bounded universal approximators and extend the approximation result to a family of equally competent networks. Furthermore, with generalization bound theory, we show that the proposed shortcut topology enjoys excellent generalizability. Finally, we corroborate our theoretical analyses by comparing the proposed topology with popular architectures, including ResNet and DenseNet, on well-known benchmarks and perform a saliency map analysis to interpret the proposed topology. Our work helps enhance the understanding of the role of shortcuts and suggests further opportunities to innovate neural architectures.
PDF Abstract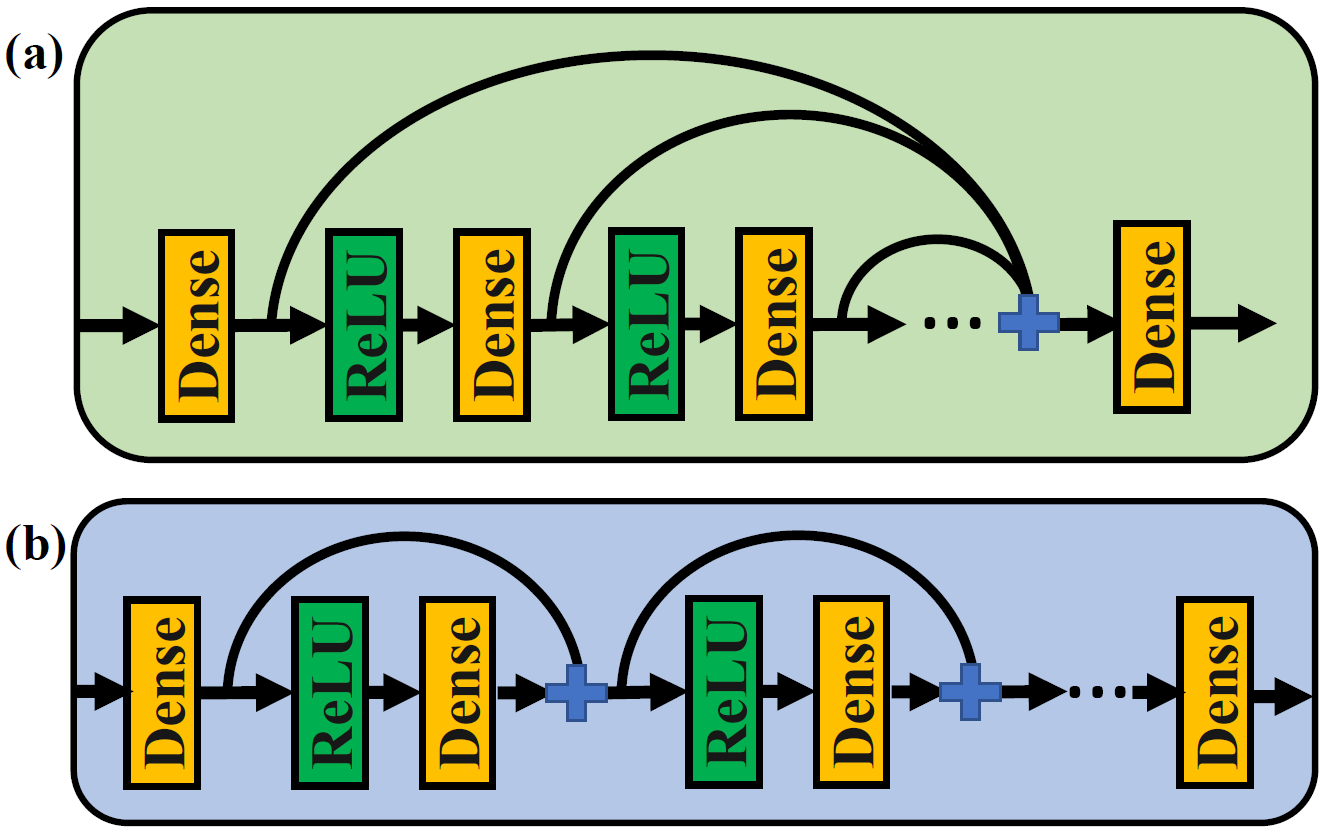

 ImageNet
ImageNet