Regularization
Regularization
L1 Regularization
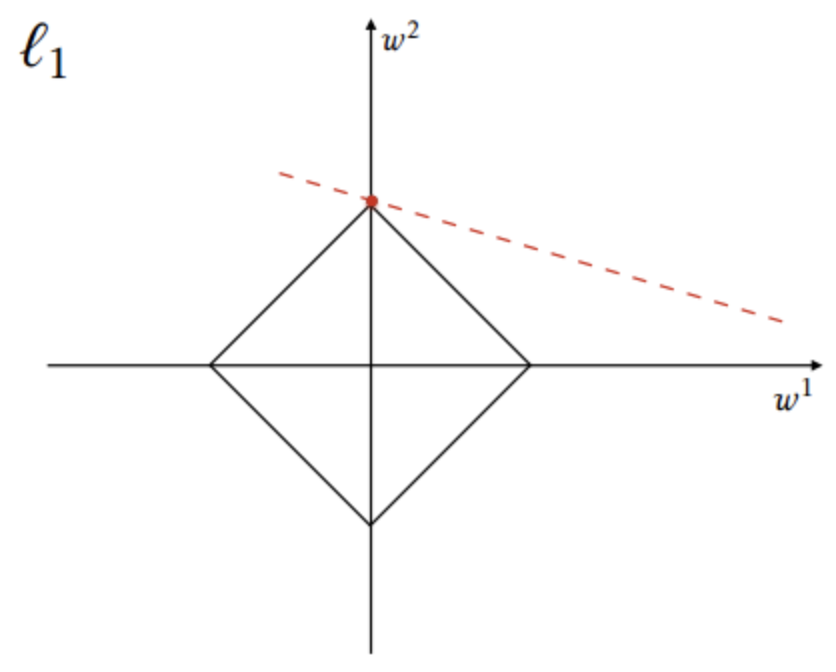
$L_{1}$ Regularization is a regularization technique applied to the weights of a neural network. We minimize a loss function compromising both the primary loss function and a penalty on the $L_{1}$ Norm of the weights:
$$L_{new}\left(w\right) = L_{original}\left(w\right) + \lambda{||w||}_{1}$$
where $\lambda$ is a value determining the strength of the penalty. In contrast to weight decay, $L_{1}$ regularization promotes sparsity; i.e. some parameters have an optimal value of zero.
Image Source: Wikipedia
Papers
| Paper | Code | Results | Date | Stars |
|---|
Tasks
| Task | Papers | Share |
|---|---|---|
| Language Modelling | 5 | 5.10% |
| Speech Synthesis | 4 | 4.08% |
| Translation | 3 | 3.06% |
| Time Series Analysis | 3 | 3.06% |
| BIG-bench Machine Learning | 3 | 3.06% |
| Object Detection | 3 | 3.06% |
| Decoder | 2 | 2.04% |
| Image Classification | 2 | 2.04% |
| Recommendation Systems | 2 | 2.04% |
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
| 🤖 No Components Found | You can add them if they exist; e.g. Mask R-CNN uses RoIAlign |