Activation Functions
Activation Functions
S-shaped ReLU
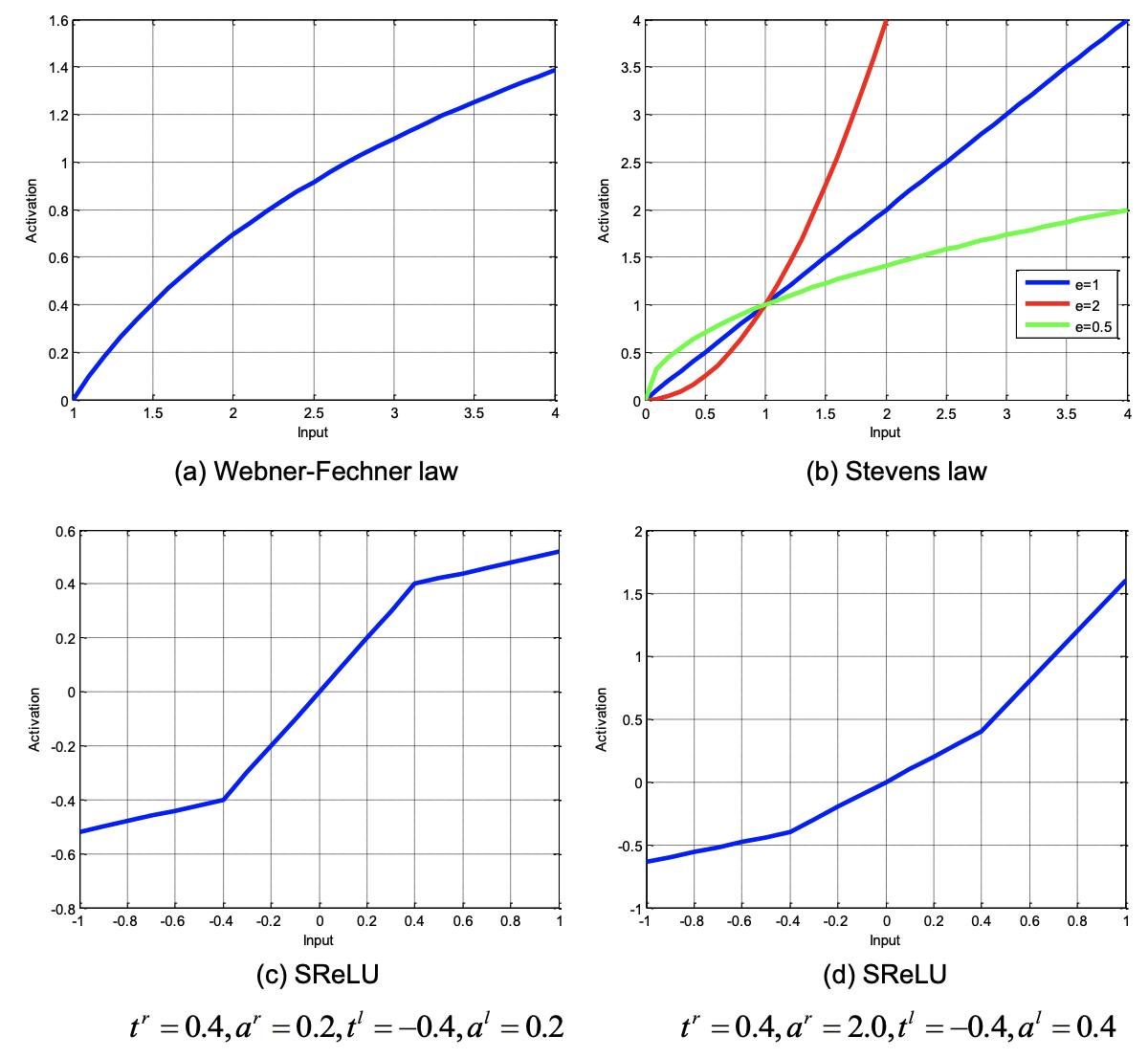
Introduced by Jin et al. in Deep Learning with S-shaped Rectified Linear Activation UnitsThe S-shaped Rectified Linear Unit, or SReLU, is an activation function for neural networks. It learns both convex and non-convex functions, imitating the multiple function forms given by the two fundamental laws, namely the Webner-Fechner law and the Stevens law, in psychophysics and neural sciences. Specifically, SReLU consists of three piecewise linear functions, which are formulated by four learnable parameters.
The SReLU is defined as a mapping:
$$ f\left(x\right) = t_{i}^{r} + a^{r}_{i}\left(x_{i}-t^{r}_{i}\right) \text{ if } x_{i} \geq t^{r}_{i} $$ $$ f\left(x\right) = x_{i} \text{ if } t^{r}_{i} > x > t_{i}^{l}$$ $$ f\left(x\right) = t_{i}^{l} + a^{l}_{i}\left(x_{i}-t^{l}_{i}\right) \text{ if } x_{i} \leq t^{l}_{i} $$
where $t^{l}_{i}$, $t^{r}_{i}$ and $a^{l}_{i}$ are learnable parameters of the network $i$ and indicates that the SReLU can differ in different channels. The parameter $a^{r}_{i}$ represents the slope of the right line with input above a set threshold. $t^{r}_{i}$ and $t^{l}_{i}$ are thresholds in positive and negative directions respectively.
Source: Activation Functions
Source: Deep Learning with S-shaped Rectified Linear Activation UnitsPapers
| Paper | Code | Results | Date | Stars |
|---|
Usage Over Time
Components
| Component | Type |
|
|---|---|---|
| 🤖 No Components Found | You can add them if they exist; e.g. Mask R-CNN uses RoIAlign |