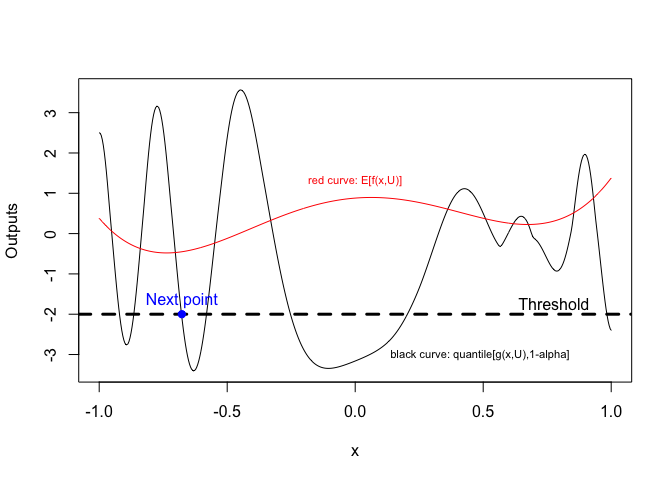
A sampling criterion for constrained Bayesian optimization with uncertainties
We consider the problem of chance constrained optimization where it is sought to optimize a function and satisfy constraints, both of which are affected by uncertainties. The real world declinations of this problem are particularly challenging because of their inherent computational cost. To tackle such problems, we propose a new Bayesian optimization method. It applies to the situation where the uncertainty comes from some of the inputs, so that it becomes possible to define an acquisition criterion in the joint controlled-uncontrolled input space. The main contribution of this work is an acquisition criterion that accounts for both the average improvement in objective function and the constraint reliability. The criterion is derived following the Stepwise Uncertainty Reduction logic and its maximization provides both optimal controlled and uncontrolled parameters. Analytical expressions are given to efficiently calculate the criterion. Numerical studies on test functions are presented. It is found through experimental comparisons with alternative sampling criteria that the adequation between the sampling criterion and the problem contributes to the efficiency of the overall optimization. As a side result, an expression for the variance of the improvement is given.
PDF Abstract