An Efficient Solution to Non-Minimal Case Essential Matrix Estimation
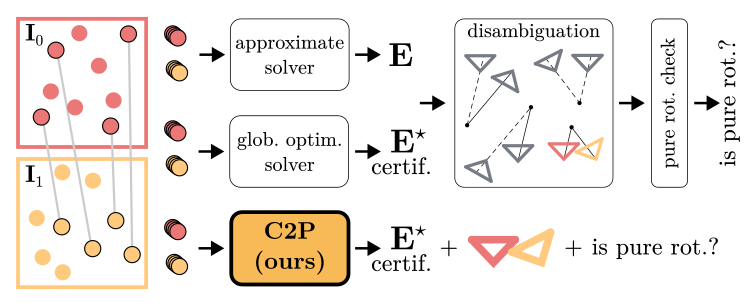
Finding relative pose between two calibrated images is a fundamental task in computer vision. Given five point correspondences, the classical five-point methods can be used to calculate the essential matrix efficiently. For the case of $N$ ($N > 5$) inlier point correspondences, which is called $N$-point problem, existing methods are either inefficient or prone to local minima. In this paper, we propose a certifiably globally optimal and efficient solver for the $N$-point problem. First we formulate the problem as a quadratically constrained quadratic program (QCQP). Then a certifiably globally optimal solution to this problem is obtained by semidefinite relaxation. This allows us to obtain certifiably globally optimal solutions to the original non-convex QCQPs in polynomial time. The theoretical guarantees of the semidefinite relaxation are also provided, including tightness and local stability. To deal with outliers, we propose a robust $N$-point method using M-estimators. Though global optimality cannot be guaranteed for the overall robust framework, the proposed robust $N$-point method can achieve good performance when the outlier ratio is not high. Extensive experiments on synthetic and real-world datasets demonstrated that our $N$-point method is $2\sim3$ orders of magnitude faster than state-of-the-art methods. Moreover, our robust $N$-point method outperforms state-of-the-art methods in terms of robustness and accuracy.
PDF Abstract